计算机组成原理(02318) 第二章 数据的表示与运算
课程内容
其他知识点
原码/反码/补码/移码
- 正数的原码是其二进制本身, 负数的原码是其正数原码的基础上符号位为1其余位不变; 0的原码有两种表示:0000 0000和1000 0000
- 正数的反码是其二进制本身, 负数的反码是其负数原码的基础上符号位不变其余位取反; 0的反码有两种表示:0000 0000和1000 0000
- 正数的补码是其二进制本身, 负数的补码是其负数反码的基础上符号位不变末位加一; 0的补码只有一种表示:0000 0000, 而1000 0000表示的是-128
- 正数和负数的移码都是其补码的符号位取反; 1000 0000 和 1111 1111 保留用来表示特殊值和无穷大
- 参考
考核知识点及考核要求
主要复习知识点
- 数制和编码
- 真值和机器数的含义及其相互关系、定点数的原码/补码/反码和移码四种编码方式
- 各类进位记数制数据之间的转换、真值和机器数(编码)之间的转换
- 整数的表示
- 无符号整数的用途和表示,带符号整数的表示,计算机用补码表示带符号整数的原因,模运算系统的本质
- 解释和解决高级语言程序中整数类型数据的表示和转换问题
- 实数的表示
- 浮点数的表示格式及其表示精度和表示范围之间的关系/规格化浮点数的概念和浮点数规格化方法,IEEE 754标准
- 能再真值与单精度格式浮点数之间转换/解释和解决高级语言程序中浮点数类型数值的表示和转换问题
- 非数值的数据的编码表示
- 逻辑数据/西文字符和汉字字符的常用表示方法(ASCII码,GB 2312)
- 数据的宽度和存储
- 常用数据长度单位的含义(bit,Byte,KB,MB,GB,TB…)
- 能够利用对大端和小端排列方式以及数据对其方式的理解,来计算高级语言程序中变量的地址以及所占空间大小等
- 数据校验码
- 校验码的含义/奇偶校验的基本原理/海明校验的基本思想/循环冗余校验码(CRC)的含义
- 能够对给定数串计算奇偶校验位
- 加法器和算术逻辑部件
- 半加器/全加器/加法器/算术逻辑部件(ALU)/溢出标志OF/进位标志CF/符号标志SF/零标志ZF
- 带标志加法器的结构和功能/补码加减法运算其的结构和功能
- 能够对给定两个变量再带符号加法器以及补码加减法运算器中进行运算,并对结果进行解释和说明
- 定点乘法运算
- 无符号乘运算基本原理,定点原码乘运算基本原理,定点补码乘运算基本原理
- 能够根据相应乘运算原理对给定两个数计算出乘积的机器数及其真值
- 定点除法运算
- 无符号除运算基本原理,定点原码除运算基本原理,定点补码除运算基本原理
- 能够根据相应除运算原理对给定两个数计算出商和余数的机器数及其真值
- 浮点数运算
- 浮点数加减法运算过程,IEEE 754标准对附加位的添加以及舍入模式等方面的规定,了解浮点数乘法和除法运算的基本思想
- 对给定两个浮点数进行加减运算
重点难点
- 重点
- 无符号数的表示/带符号数的补码表示/IEEE 754浮点数标准/定点数的移位运算/整数的加减运算/浮点数的加减运算/ALU功能和实现
- 难点
- IEEE浮点数的表示范围/特殊数(NaN,无穷大等)的浮点数表示/定点乘法运算/定点除法运算/浮点数乘除法运算
2.1 数制和编码
2.1.1 信息的二进制编码
- 计算机内部信息使用二进制数字表示的原因:
- 二进制只有两种基本状态, 使用有两个稳定状态的额物理期间可以容易表示二进制数的每一位.
- 二进制的编/计数和运算规则简单, 可用开关电路实现, 简便易行.
- 两个符号
0和1正好与逻辑命题的两个值真和假相对应, 为计算机实现逻辑运算和程序中的逻辑判断提供便利条件, 特别是能通过逻辑门电路方便实现算术运算
- 指令处理的数据分为两种:
数值数据和非数值数据. 计算机内部,整数用定点数表示,实数用浮点数表述- 数值数据 : 表示数量的多少, 可比较大小, 分整数(又分带符号和无符号)和实数.
- 非数值数据 : 无大小之分, 不表示数量多少, 主要包括字符数据和逻辑数据
- 在计算机内部如果采用十进制表示数值数据的话,需要将十进制编码成二进制数, 即采用 二进制编码的十进制数(Binary Coded Decimal Number,BCD) 表示.
- 表示一个数值数据要确定三个要素, 任何给定的一个二进制
0/1序列, 未确定采用什么进位记数制/定点还是浮点表示以及编码表示方法之前, 它所代表的数值数据的值是无法确定的:- 进位记数制
- 定/浮点表示
- 编码规则.
2.1.2 进位记数制
-
任意十进制数值计算公式
$$ D=d_nd_{n-1}…d_1d_0d_{-1}d_{-2}…d_{-m}(m,n为整数) $$
-
其中值为: \( V(D)=d_nx10^n+d_{n-1}x10^{n-1}+…+d_0x10^0+d_{-1}x10^{-1}+d_{-2}x10^{-2}+d_{-m}x10^{-m} \), 其中的 \(d_i(i=n,n-1,…,1,0,-1,-2,…,-m)\)可以是0-9十个数字任意一个
-
10称为 基数 ,代表每个数位上可以使用的不同数字符号个数. \(10^i\)称为第i位的 权 , 十进制数运算时, 每位计满十之后要向高位进一, 逢十进一. -
二进制的基数是
2, 各位只能使用数字符号0和1, 采用逢二进一, 第i位上的权是 \(2^i\).- 例子 : 二进制数(100101.01)代表的值是
- \(100101.01_2=1x2^5+0x2^4+0x2^3+1x2^2+0x2^1+1x2^0+0x2^{-1}+1x2^{-2}=37.25_{10} \)
- \(2^{-1}=1/2=0.5 2^{-2}=1/2/2=0.25\)
- 一个任意二进制可以表示为 $$ V(B)=b_nx2^n+b_{n-1}x2^{n-1}+b_0x2^0+b_{-1}x2^{-1}+b_{-m}x2^{-m} $$
-
扩展到
R进制数字系统中, 应采用R个基本字符(0,1,2,…,R-1)表示各位上的数字, 采用"逢R进一"的运算规则, 对于每一个数位i, 该位上的权为\(R^{i}\),R被称为该数字系统的基. -
计算机中常见记数制:
- 二进制, R=2, 基本符号为0和1, 用 B(Binary) 表示
- 八进制, R=8, 基本符号为0-7, 用 O(Octal) 表示
- 十进制, R=10, 基本符号为0-9, 用 D(Decimal) 表示
- 十六进制, R=16, 基本符号为0-f, 用 H(Hexadecimal) 表示, 有时也使用 0x 前缀
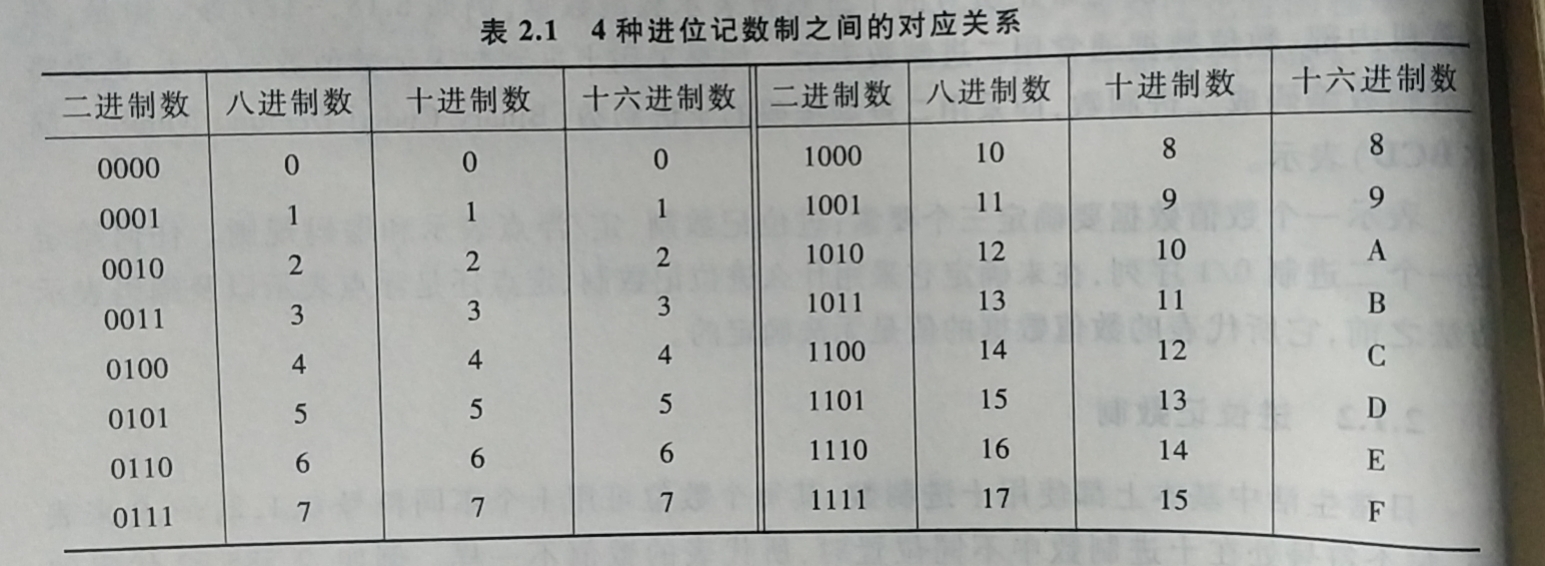
-
计算机内部所有信息都用二进制编码表示. 在外部为方便书写和阅读则采用八进制十进制十六进制.
- R进制数转换十进制数
-
二进制数
10101.01转换成十进制 $$ 10101.01_2 = 1x2^4+0x2^3+1x2^2+0x2^1+1x2^0+0x2^{-1}+1x2^{-2} = 16+0+4+0+1+0+0.25 = 21.25_{10} $$ -
八进制数
307.6转换成十进制 $$ 307.6_8 = 3x8^2+0x8^1+7x8^0+6x8^{-1} = 199+0+7+0.75 = 199.75_{10} $$ -
十六进制数
3A.C转换成十进制 $$ 3A.C_{16} = 3x16^1+10x16^0+12x16^{-1} = 48+10+0.75 = 58.75_{10} $$
- 十进制数转换R进制数
任何十进制数转换成R进制数, 要将整数和小数分别转换
- 整数部分转换
- 整数部分的转换方法是 “除基取余,上右下左”. 即, 用要转换的十进制整数去除以基数R, 将得到的余数作为结果数据中各位的数字,直到余数为0为止. 上面的余数(先得到的余数)作为右边低位上的数位,下面的余数作为左边高位上的数位.

- 小数部分转换 : 一个数的负次方等于这个数的正次方的倒数,例如:2的(-3)次方等于2的3次方的倒数即1/8
- 小数部分转换方式是 “乘基取整,上左下右”. 即, 用要转换的十进制小数去乘以基数R, 将得到的乘积整数部分作为结果数据中各位的数字, 小数部分继续与基数R相乘. 以此类推, 直到某步乘积的小数部分为0或已得到希望的位数位置. 最后将上面的整数部分作为左边高位上的数位, 下面的整数部分作为右边地位上的数位.(在转换过程中可能乘积的小数部分总得不到0,即转换得到希望的位数后还有余数,该种情况下得到的是近似值) 例子:将十进制小数 0.6875分别转换成八进制和二进制
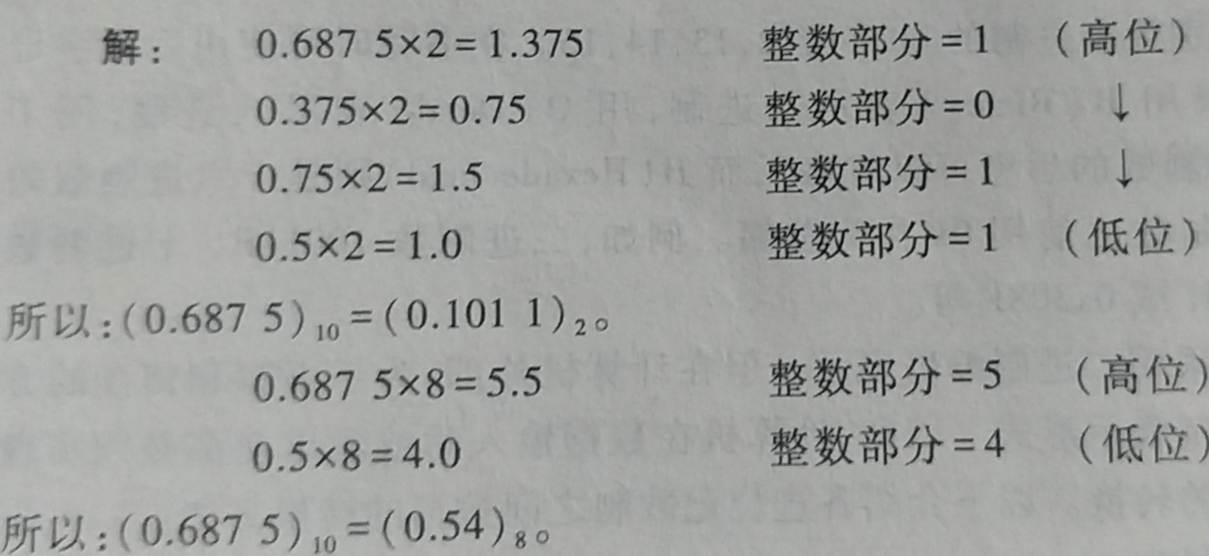


- 二,八,十六进制互相转换
-
八进制和二进制之间的转换 : 只要将每一个八进制数字改写成等值3位二进制即可, 且保持高低位次序不变. \(0_8 = 000_2\)
\(1_8 = 001_2\)
\(2_8 = 010_2\)
\(3_8 = 011_2\)
\(4_8 = 100_2\)
\(5_8 = 101_2\)
\(6_8 = 110_2\)
\(7_8 = 111_2\)
例子: (13.724)O 转成 二进制 13.724O=001 011. 111 010 100=1011.1110101- 十六进制和二进制之间的转换 : 方法与八进制转二进制类似, 等值4位即可,高低位次序不变.
例子: (2B.5E)H 转成 二进制 0X2B.5E=0010 1011 . 0101 1110 = 101011.0101111B
2.1.3 定点数的编码表示
- 定点数编码表示方法有以下四种.
- 原码
- 补码
- 反码
- 移码
- 参考链接:原码, 反码, 补码 详解
- 数值数据在计算机内部编码表示的数称为 机器数 , 而机器数
真正的值(现实中带有正负符号的数)称为机器数的 真值 . 机器数一定是一个0/1序列, 通常缩写成十六进制. - 假设机器数X的真值为 \( X_T 的二进制形式(X_i'=0或1)如下 \) :
-
X为定点整数时 : \( X_T = ±X_{n-2}'…X_1’X_0' \)
-
X为定点小数时 : \( X_T = ±0.X_{n-2}'…X_1’X_0' \)
-
对 \( X_T用n位二进制数编码后, 机器数X表示为 : X=X_{n-1}X_{n-2}…X_{1}X_{0} \)
-
机器数X的位数为n, 其中第一位 \( X_{n-1} \) 是
数符 ,后面的n-1是 数值部分
-
- 数值数据在计算机内部的编码问题实际就是机器数X的各位\( X_i \) 的取值与真值X的关系问题.
- 原码表示法
- 原码由符号位直接跟数值位构成, 也称"符号-数值(sign and magnitude)“表示法. 仅符号位不同, 数值部分完全相同.
- 两种表示形式:
- \ ([+0]_{原} = 0 000 … 0 \)
- \ ([-0]_{原} = 1 000 … 0 \)
- 例子 :
真值-10(-1010B),则用8位原码表示的机器数为 : 1000 1010B(8AH/0x8A) 真值-0.625(-0.101B), 则用8位原码表示的机器数位 : 11010000B(D0H/0xD0)- 原码的优点 :
- 与真值对应关系值观方便, 且与真值转换简单.
- 原码的缺点 :
- 零的表示不唯一, 使用不便, 且加减运算规则复杂, 要判定是否两个异号数相加或是两个同号数相减, 若是则必须判定两个数的绝对值大小, 根据判断结果决定结果符号, 并用绝对值大的数减小的数. 现代计算机不用原码表示整数, 只用定点原码小数来表示浮点数的尾数部分.
- 补码表示法
- 补码可以实现加减运算统一(用加法实现减法运算). 也称"2-补码(two’s complement)“表示法, 由符号位后跟上真值的模\(2^n\)构成.
- 额外知识 :
- 模运算 : 在模运算系统中, 若A,B,M满足关系 : A = B + K x M(K为整数), 则记为: \( A \equiv B (mod M) \), 即A,B各除以M后的余数相同, 故称 B和A为 模M 同余, 也就是在一个模运算系统中, 一个数与它除以"模"后得到的余数是一样的.
A = B + K x M A ≡ B (Mod M) 123 = 3 + 20 x 6 123 ≡ 3(mod 6), 123 % 6 = 3 123 / 20 = 6 ... 3 3 / 20 = 0 ... 3书本的例子1: 钟表是一个典型的模运算系统, 模数为12. 假定钟表时针指向10点, 要将它拨向6点, 则有两种拨法 : 1. 倒拨4格 : 10-4 = 6 2. 顺拨8格 : 10+8=18 (18≡6(mod 12)) 所以在模12系统中, 10-4≡10+(12-4)≡10+8(mod 12), 即: -4≡8(mod 12). 我们称8是-4对模12的补码(需要参照模12运算系统理解), 同样有 -3≡9(mod 12), -5≡7(mod 12)等. 上述的例子与同余的概念得知结论: 对于某一个确定的模, 某数A减去小于模的另一数B, 可以用A加上-B的补码来代替. 这就是补码可以借助加法运算实现减法运算的原因. 18≡6(mod 12) = 6 - 18 = 12 -3≡9(mod 12) = 9 - (-3) = 12 -5≡7(mod 12) = 7 - (-5) = 12 -8≡4(mod 12) = 4 - (-8) = 12 书本例子2: 假定在钟表上只能顺时针拨动时针, 则如何用该方式实现将10点倒拨4格让时针指向6点. 解: 首先时钟是一个模为12的模运算系统, 因为10-4 ≡ 10+(12-4)≡10+8≡6(mod 12), 所以顺时针拨动8格实现 个人理解: 首先10点逆时针拨动4格是回到六点, 10+(12-4)=18,此时时针18又指向6点, 故在模12运算系统中, 6/18≡6(mod 12), 6和18是6模12的余. 8是-4对模12的补码(在10点时,顺时针拨动8格等于逆时针拨动4格), 所以-4≡8(mod 12), 还有-3≡9(mod 12)... 书本例子2: 假定算盘只有4档, 且只能做加法, 如何用算盘计算 9828-1928的结果? 解: 该算盘是一个"4位十进制"模运算系统, 其模为10的4次方.(10*10*10*10). 9828-1928≡9828+(10000-1928)≡9828+8072≡7900(mod 10000), 所以可用9828+8072(-1928的补码)实现9828-1928的功能. 在4档十进制算盘中, 如果结果超过4位, 则高位会被舍弃, 只留下低位4位表示结果, 留在算盘上的值相当于模10的4次方的值. 推广到计算机内部, n位运算部件相当于只有n档二进制算盘, 其模是2的n次方.- 计算机的存储/运算和传送部件都只有有限位, 相当于有限档数的算盘, 因此计算机所表示的机器数的位数也只有有限位. 两个n位二进制运算可能产生一个多于n位的数, 计算机也会舍弃高位保留低n位作为结果:
- 剩下的低n位不能正确表示运算结果, 即丢掉的高位也是运算结果的一部分. 当两个同号数相加时得出的结果是n位数的范围无法表示该结果时, 则称为 “溢出(overflow)" 现象.
- 剩下的低n位能正确表示运算结果, 即丢掉的高位不影响运算结果. 在两个同号数相减或两个异号数相加时, 运算结果即使舍弃高位数也可能不会影响运算结果. 舍去高位的操作相当于 “将一个多于n位的数去除以\(2^n\)”, 保留余数作为结果, 也就是 模运算 操作.(参考书本例子2)
- 补码的定义
- 根据同余的概念以及数的互补关系, 得出补码表示方法:
- 正数的补码是它本身.
- 负数的补码等于模与该负数绝对值之差.
- 因此, 数\( X_T \) 的补码可用以下公式表示
- 当\( X_T \)为正数时, \( [X_T]_补 = X_T = M + X_T (mod M) \)
- 当\( X_T \)为负数时, \( [X_T]_补 = M - |X_T| = M + X_T (mod M) \)
- 根据以上得知结论, 对于任意一个数\( X_T ,[X_T]_补 = M + X_T (mod M) \)
- 具有一位符号位和n-1位数值位的n位补码定义如下: \( [X_T]_补 = 2^n + X_T (-2^{n-1} ≤ X_T < 2^{n-1}, mod 2^n) \)
- 因此n位补码的最大可能表示值为 \( +(2^{n-1}-1), 最小值表示值为 -2^{n-1} \)
- 根据同余的概念以及数的互补关系, 得出补码表示方法:
- 特殊数据的补码表示
- 当补码的位数为n位时, 其模为\(2^n\)
- \( [-2^{n-1}]_补 = 2^n-2^{n-1}=2^{n-1}=1 0…0(n-1个0)(mod 2^n) \)
- 当补码位数为n+1位时, 其模为 \( 2^{n+1} \)
- \( [-2^{n-1}]_补 = 2^{n+1}-2^{n-1}=2^n+2^{n-1}=1 0…0(n-1个0)(mod 2^{n+1}) \)
- 从以上例子可以看出, 同一个真值在不同位数的补码表示中, 其对应的机器数不同.
- 因此在给定编码表示时, 一定要明确编码的位数.
- 在及其内部, 编码的位数就是机器中运算部件的位数, 即机器字长
例子1: 假设补码位数为n, 求-1的补码表示 解: 根据补码定义, 有 : [-1](补码) = 2的n次方-1 = 11..1(n个1) 例子2: 求0的补码表示 解: 根据补码定义, [+0](补码)=[-0](补码)=2的n次方±0=100...0=000..0(mod 2的n次方) 由上述结果得知, 0的补码是唯一的. ①减少了+0和-0之间的转换 ②少占用一个编码表示, 使补码比原码能多一个最小负数. 在n位原码定点数中, 100...0用来表示-0, 但在n位补码表示中, -0和+0都用000..00表示, 而100..00表示最小负数-2的n-1次方 - 补码与真值之间的转换方法
- 原码与真值之间转换简单, 只要对符号位转换, 数值部分不需要改变. 而正数的补码与原码一样, 但负数转换规则不同.
假设补码的位数为8, 求1101100和-1101100的补码表示 补码的位数为8, 说明数值位为7位. 1101100的补码 = 100000000(2的八次方)+1101100=01101100(mod 2的八次方)(位数为8,结果实际为101101100,舍弃高位1) -1101100的补码 = 100000000(2的八次方)-1101100=10000000+100000000-1101100=10000000+(1111111-1101100)+1=10000000+0010011+1=10010100(mod 2的八次方)
- 以上例子可得出, 正数的补码为其本身, 负数的补码在正数的基础上, 符号位为1数值位取反后加1.
- 由补码求真值的方法 :
- 若符号位为0, 则真值符号为正, 数值部分不变;
- 若符号位为1, 则真值符号为负, 数值部分由补码的"各位取反末位加1"得到
补码求真值例子 : 补码(1 0110100), 符号位为1所以真值符号为负, 数值部分取反得 1001011 后 加1 得 真值-1001100 求补码X=10110100的[-X]的补码 = 01001011+1 = 01001100 溢出的例子 补码X=1 0000000 求[-X]的补码 01111111+1 = 10000000(结果溢出), 得出的结果对应的是最小负数-2的7次方, 对其取负后的值为2的7次方(128), 而8位二进制能表示最大的正数为2的7次方-1(127), 因而结果太大, 8位二进制无法表示, 导致结果溢出
- 额外知识 :
- 补码可以实现加减运算统一(用加法实现减法运算). 也称"2-补码(two’s complement)“表示法, 由符号位后跟上真值的模\(2^n\)构成.
- 反码表示法
- 正数的反码还是其本身
- 负数的补码采用"各位取反,末位加1"的方法得到, 而负数的反码则各位取反不加1即可.
- 负数反码的定义就是在相应的补码表示中在末位减1.
- 反码表示存在以下几个不足:
- 0的值不唯一
- 表数范围比补码少一个最小负数
- 运算时必须考虑循环进位
- 反码很少在计算机中使用, 有时用作数码变换的中间表示形式
- 移码表示法
- 浮点数表示一个数值数据时, 实际是用两个定点数表示的
- 一个定点小数表示 浮点数的尾数
- 一个定点正数表示 浮点数的阶(指数)
- 一般请款下浮点数的 阶 都用 移码(阶码) 的编码方式表示
- 阶(指数) 指的是真值, 阶码指的是机器数, 是一个0/1序列
- 使用移码表示阶的原因:
- 因为阶E可以是正数也可以是负数, 进行浮点数加减运算时必须先对阶(比较两个数阶的大小并使之相等).
- 为简化比较操作, 使操作过程不涉及阶的符号, 可对每个阶都加上一个正的常熟, 称为偏置常数(bias), 使所有阶都转换成正整数, 这样, 在对浮点数的阶比较时就是对两个正整数比较, 因而可以直观地将两个数位从左到右对比, 简化"对阶"的操作.
- 假设用来表示阶E的移码的位数为n, 则 \( [E]_移 = 偏置常数+E, 通常偏置常数取 2^{n-1}或2^{n-1}-1 \)
- 浮点数表示一个数值数据时, 实际是用两个定点数表示的
2.2 整数的表示
- 整数的小数点隐含在数的最右边, 无需表示小数点, 因为也被称为定点数
- 计算机处理的整数可用二进制表示, 也可以用二进制编码的十进制数(BCD码)表示
- 二进制整数分为
无符号整数(unsigned integer)和带符号整数(signed integer)
2.2.1 无符号整数的表示
- 当一个编码的所有二进位都用来表示数值而没有符号位时, 该编码就是无符号整数, 为正整数或非负整数
- 一般在全部正数运算且不出现负数结果的场合下使用无符号整数
- 可用无符号整数进行地址运算, 或用来表示指针
- 在字长相同的情况下能表示最大数比带符号整数所能表示的大, n位无符号整数可表示数的范围位 \( 0~2^n-1 \)
- 8位无符号整数能表示 \( 0~2^8-1, 00000000B~11111111B, 最大数为255, 而带符号整数最大数是127 \)
2.2.2 带符号整数的表示
- 也称有符号整数. 必须用一个二进制数来表示二进制符号.
- 二进制定点数编码表示(原码, 补码, 反码和移码)都可以表示带符号整数, 但补码更能突出其优点:
- 与原码反码相比, 数0的补码表示形式唯一
- 补码运算系统是一种模运算系统, 可用加法实现减法运算, 且符号位也可以和数值位一起参加运算
- 补码比原码和反码多表示一个最小负数
- 与反码相比, 不需要通过循环进位来调整结果
- 现代计算机中带符号整数都用补码表示, 故n位带符号整数克表示的数值范围为\( -2^{n-1} ~ 2^{n-1}-1 \)
- 例如8位带符号整数可表示范围为 : -128 ~ +127
2.2.3 C语言中的整数类型
- C语言中允许无符号整数和带符号整数之间转换, 转换后数的真值是将原二进制机器数按转换后的数据类型重新解释得到的.
#include <stdio.h>
int main()
{
int x = -1;
unsigned u = 2147483648;
// x=4294967295=-1
// -1的补码为 : 111...1, 在当作32位无符号数来解释时, 其值为2^32-1 = 4294967296-1 = 4294967295
// u=2147483648=-2147483648
// 2^31的无符号数表示为 100...0, 当这个数被解释为32位带符号整数时, 其最小值为:-2^{32-1} = -2147483648
printf("x=%u=%d\n",x,x);
printf("u=%u=%d\n",u,u);
return 0;
}
- 在C语言中, 执行一个运算同时有无符号和带符号整数参加, 那么C语言编译器会隐含地将带符号转为无符号, 因为会带来意想不到的结果.

2.3 实数的表示
- 计算机内部进行数据存储/运算和传送的部件位数有限, 因而用定点数表示数值数据时其表示范围很小; 对于n位带符号整数其表示范围为\( -2^{n-1} ~ 2^{n-1}-1 \), 运算结果很容易溢出
- 定点数无法表示大量带有小数点的实数, 因此计算机专门用浮点数表示实数
2.3.1 浮点数的表示形式
- 对于任意一个实数, 可以表示为 : \( X = (-1)^s x M x R^E \)
- 其中S取值0或1, 用于决定X的符号, 一般0表示正1表示负
- M是一个二进制定点小数, 称为数X的尾数
- E是一个二进制定点整数, 称为数X的阶或指数
- R是基数, 可以约定为2,4,16等
- 要确定一个实数的值, 只要在默认基数R下确定数符S, 尾数M和阶E即可;
- 浮点数格式秩序规定
S,M,E各自所用位数, 编码方式和所在位置, 而基数R与定点数小数点位置一样是默认的 - 一般尾数M用定点原码小数表示, 阶E用移码表示
- IEEE 754浮点数标准被广泛使用之前不同计算机所用的浮点数表示格式各不相同.
将十进制数65798转换为下述32位浮点数格式
(0位为数符位S,1-8位为8位位移码表示的阶码E(偏置常数位128),9-31位为24位二进制原码小数表示的尾数,基数为2, 规格化尾数形式为±0.1bbbbbb...b, 其中小数点后第一位1不显式地表示出来, 这样可用23个数位表示24位尾数)
解答:
65798的二进制为(1 0000 0001 0000 0110)=(0.1000 0000 1000 0011 0)x2的17次方,
数符S=0, 阶码E=(128+17)=145=二进制(1001 0001)
所以十进制65798的浮点数形式表示为
0 10010001 00000001000001100000000(十六进制表示形式 : 48 80 83 00H)
S(数符) E(阶) M(尾数)

- 上述格式的规格化浮点数的表示范围如下
- \( 正数最大值 : 0.11…1 x 2^{11…1}=(1-2^{-24})x2^127 \)
- \( 正数最小值 : 0.10…0 x 2^{00…0}=(1/2)x2^{-128}=2^{-129} \)
- 因为原码是关于原点对称的, 故该浮点格式的范围是关于原点对称的. 数轴上有4个区间的数不能用浮点数表示, 这些区间称为溢出区, 接近0的区间为下溢区, 向无穷大方向延申的区间称为上溢区.

2.3.2 浮点数的规格化
- 浮点数尾数的尾数决定浮点数的有效位数, 有效数位越多数据精度越高.
- 浮点数规格化 : 保证浮点数运算过程尽可能多保留有效数字位数, 让有效数字尽量占满尾数数位, 且能让浮点数表示具有唯一性
- 浮点数基数为2, 尾数规格化的浮点数形式应为 \( ±0.1bb…bx2^E(这里b是0或1) \)
- 规格化操作有两种, 当有效数位进到小数点前面时需要进行右规; 当出现形如\( ±0.0…0bb…bx2^E \)的运算结果时, 需要进行左规
- 右规 : 尾数每右移1位阶码加1, 直到尾数变成规格化形式为止; 右规时阶码会增加, 因此阶码有可能溢出
- 左规 : 尾数每左移1位阶码减1, 直到尾数变成规格化形式位置.
2.3.3 IEEE 754浮点数标准
-
目前几乎所有计算机都采用 IEEE 754 标准表示浮点数. 该标准中提供两种基本浮点数格式
- 32位单精度 : 1位符号
s, 8位阶码e和23位尾数f - 64位双精度 : 1位符号
s, 11位阶码e和52位尾数f
- 32位单精度 : 1位符号
-
基数隐含为2; 尾数用原码表示, 尾数的第一位总为1, 可在尾数中缺省第一位的1, 称为隐藏位 , 使得单(双)精度格式的23(52)位尾数实际上代表了24(53)位有效数字
- IEEE 754规定隐藏位"1"的位置在小数点之前
-
阶用移码表示, 偏置常数并不是通常n位移码所用的 \( 2^{n-1},而是(2^{n-1}-1) \), 因此单精度和双精度的偏置常数分别是
127和1023- 单精度浮点数格式 : 阶码e=127+阶, 阶=e-127
- 阶码e的范围为
00000000~11111111, 因为具有全0阶码和全1阶码的特殊位序列是一些特殊数(下图), - 所以正常的规格化非0数的阶码范围为
00000001(最小)~11111110(最大), 得出最小的阶为,\( (00000001)_2-127=-126, 最大阶为 (11111110)_2-127=254-127=127 \), 因此对应阶码范围为 -126~127 - 对于IEEE754标准格式的数, 一些特殊的位序列(阶码为全0或全1)有特别的解释
- 阶码e的范围为
- 双精度浮点数格式 : 阶码e=1023+阶, 阶=e-1023
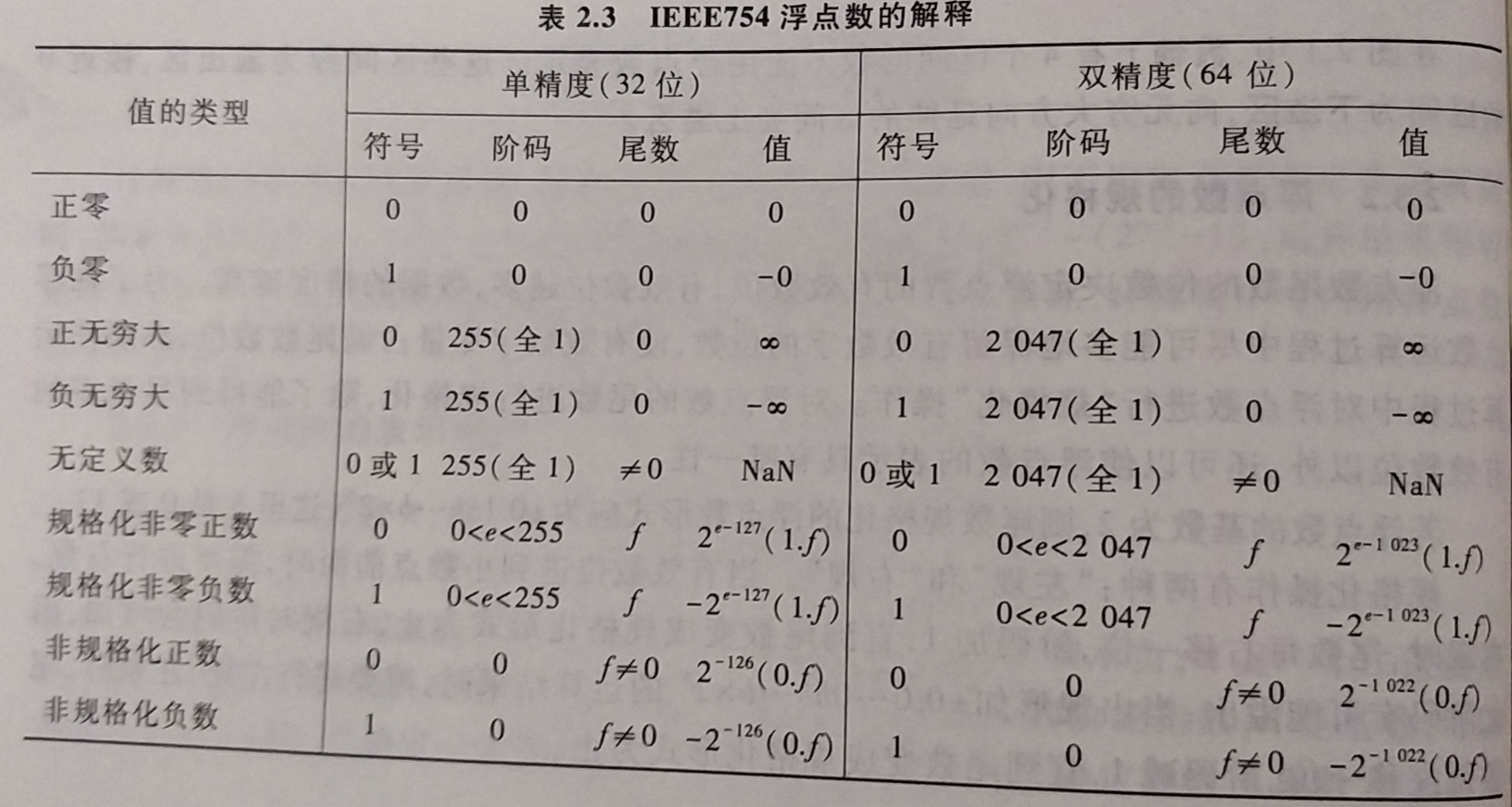
- 单精度浮点数格式 : 阶码e=127+阶, 阶=e-127
-
IEEE754规定的数进行了以下分类
-
全0阶码全0尾数 : +0/-0
- IEEE754的0有两种表示, +0和-0, 0的符号取决于
数符s. 一般+0和-0是等效的
- IEEE754的0有两种表示, +0和-0, 0的符号取决于
-
全0阶码非0尾数 : 非规格化数
- 特点是阶码部分的编码为全0, 尾数高位有一个或几个连续的0, 但不全为0
- 因此非规格化数的隐藏位为0, 且单精度和双精度的阶分别为 : -126或-1022, 故数值分别为: $$ (-1)^s x 0.f x 2^{-126} 和 (-1)^s x 0.f x 2^{-1022} $$
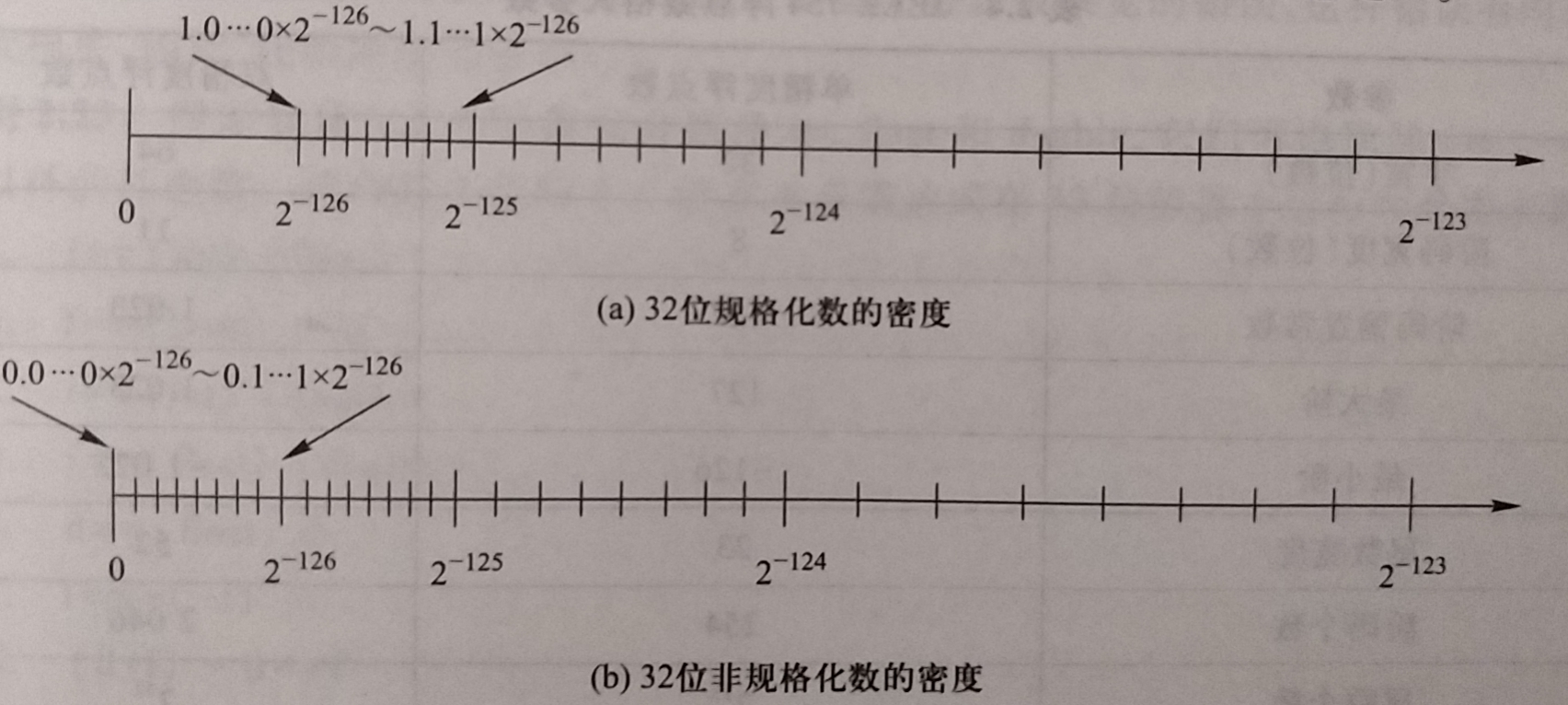
- 未定义非规格化数时32位单精度浮点数 : 在0和最小规格化数\( 2^{-126} \) 之间有一个间隙未被利用
- 定义了非规格化数后, 在0和\( 2^{-126} 之间增加了 2^{23} 个附加数, 相邻附加数之间与区间[2^{-126},2^{-125}]内的相邻数等距. \)
- 附加的 \( 2^{23}个数为非规格化数, 所有这些数据具有与区间 [2^{-126},2^{-125}]内相同的阶, 即最小阶为 2^{-126} \)
- 尾数部分变化范围为 0.00…0 ~ 0.11…1, 这里的隐含位为0, 这也是非规格化数的重要标志之一
-
全1阶码全0尾数 : +∞/-∞
- 引入无穷大数使得在计算过程出现异常的情况下程序能继续进行, 且为程序提供错误检测功能.
- 1.0/0.0的结果就是
+∞, 此结果在数值上大于所有有限数,-∞在数值上小于所有有限数 - 无穷大既可以作为操作数, 也可以作为运算结果
-
全1阶码非0尾数 : NaN (Not a Number)
- 表示一个没有定义的数, 称为 非数
- 0.0 x ∞ , (+∞)+(-∞) , \( \sqrt{x}且x<0 \) , 0.0/0.0的结果都是NaN.
- 非数分为
不发信号(quiet)和发信号(signaling)两种, 也被分别称为静止的NaN和通知的NaN - 利用NaN可以检测非初始化值的使用, 程序可用非数表示每个浮点数类型变量的非初始化值
- 利用NaN还可以使计算出现异常时程序能继续进行, 让开发者将测试或判断延迟到方便的时候进行
- 表示一个没有定义的数, 称为 非数
-
阶码非全0且非全1 : 规格化非0数
- 对于阶码范围在 1~254(单精度)和 1~2046(双精度)的数, 是一个正常的规格化非0数.
- IEEE754的定义, 这种数的阶的范围应该是 -126~127(单精度) 和 -1022~1023(双精度),计算公式分别为: $$ (-1)^s x 1.f x 2^{e-127} 和 (-1)^s x 1.f x 2^{e-1023} $$
example 1 : 将十进制数 -0.75 转换为 IEEE754的单精度浮点数格式表示 首先 -0.75的十进制转换成二进制等于 -0.11=(-1.1) x 2的-1次方 = (-1)的s次方 x 1.f x 2的e-127次方, 得出的规格化浮点数是 1 0111 1110 1000 0000...0000, 十六进制表示为 BF 40 00 00H 得出 s=1,f=0.1000..0,e=(127-1)=126=0111 1110(s=1是因为该数值是负数, 得出符号s=1,f的值是将-1.1变成-1后得到的结果,e=(127-1)是因为单精度的偏置常数是127) example 2 : 求机器数为 C0 A0 00 00H的IEEE754单精度浮点数的值 求一个机器数的真值, 就是将该值转换成十进制. 首先 C0 A0 00 00H展开为一个32位单精度浮点数格式 1 1000 0001 010 0000...0000 根据IEEE754得出符号s的值为1, 阶码e=(1000 0001)二进制=129(十进制), 尾数f部分则为, 010 0000=0.010(二进制)=0.25(十进制) 根据公式 (-1)的s次方 x 1.f x 2的e-127次方 = (-1)的1次方 x 1.25 x 2的129-127次方 = -1.25 x 2的2次方 = -5.0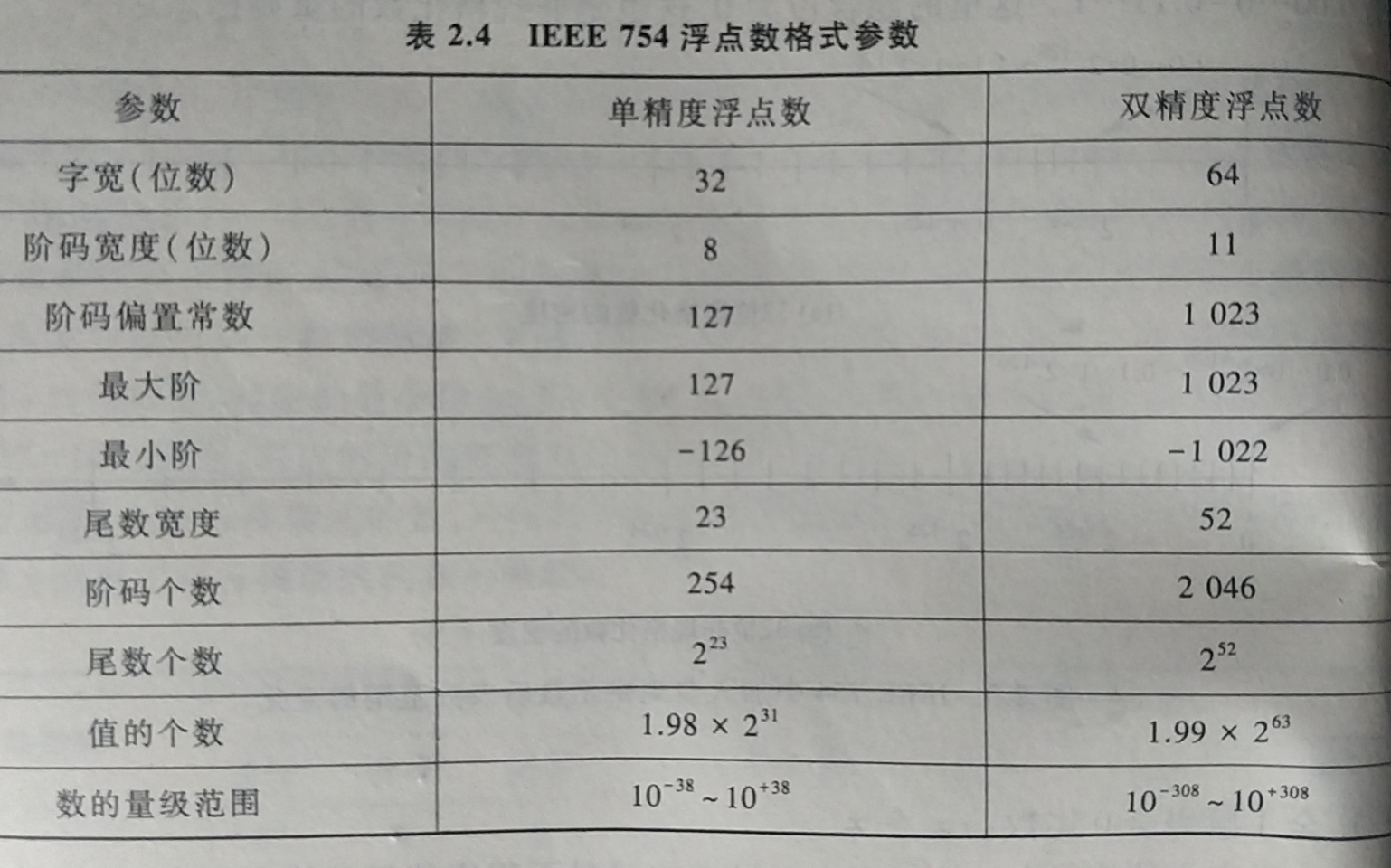
- IEEE754用全0阶码和全1阶码表示以下特殊值, 比如0, ∞和NaN, 因此除去全0和全1的阶码后, 单精度和双精度格式的阶码个数分别为 254和2046,
- 最小阶为-126和-1022, 最大阶127和1023
- 单精度规格化数的个数为 \( 254x2^{23}=1.98x2^{31} \)
- 双精度规格化数的个数为 \( 2046x2^{52}=1.99x2^{63} \)
- 根据单精度和双精度格式的最大阶分别为 127和1023, 可得出数的量级范围分别为 :
- \( 10^{-38} ~ 10^{38} \)
- \( 10^{-308} ~ 10^{308} \)
- 对于阶码范围在 1~254(单精度)和 1~2046(双精度)的数, 是一个正常的规格化非0数.
-
2.3.4 C语言中的浮点数类型
- 当在int, float和double等类型数据之间进行强制转换时将会得到以下数值转换结果(假定int为32位)
- int转float时,不会发生溢出, 但有可能有效数字会被舍入
- int/float转double时, double有效位更多, 能保留精确值
- double转float时,float表示范围小, 可能会溢出, 且float有效位变少, 数值可能被舍入
- float/double转int时, 因为int没有小数部分, 所以数据会向0方向被截断. (1.99会变成1). int表示范围更小,可能发生溢出
- 大的浮点数转换为整数可能会导致程序错误(历史上有惨痛教训)
2.4 非数值数据的编码表示
- 逻辑值, 字符等数据都是非数值数据, 在机器内部也使用二进制表示.
2.4.1 逻辑值
- 一般情况, 每个字或其他
可寻址单位(字节, 半字等)是作为一个整体数据单元看待的. - 有时候需要将一个n位数据堪称是由n个1位数据组成, 每个取值为0或1. 以这种方式看待时, 就认为是逻辑数据
- 布尔数据
- 二进制数据阵列(每项只能取值为0或1)
- 提取数据项中的某位进行"置位”/“清0"等操作
- n个二进制可表示n个逻辑值, 逻辑数据只能参与逻辑运算, 并且是按位进行的.
- 按位与
- 按位或
- 逻辑左移
- 逻辑右移
- …
- 逻辑数据和数值数据都是一串0/1序列, 在形式上没有区别, 需要通过指令的操作码类型进行识别.
- 逻辑运算指令处理的是逻辑数据
- 算术运算指令处理的是数值数据
2.4.2 西文字符
-
由
拉丁字母,数字,标点符号及一些特殊符号组成, 统称为 “字符”(character) -
所有字符的集合叫做字符集
- 字符集中每一个字符都有一个代码(二进制编码的0/1序列), 构成该字符集的
代码表, 简称码表 - 码表中的代码具有唯一性
- 字符集中每一个字符都有一个代码(二进制编码的0/1序列), 构成该字符集的
-
字符主要用于外部设备和计算机之间交换信息, 一旦确定了所使用字符集和编码方式, 计算机内部所表示的二进制代码和外部设备输入/打印和现实的字符之间就有唯一的对应关系
-
字符集有多种, 每个字符集的编码方法也有多种
-
使用最广泛的西文字符集及其编码是ASCII码(美国标准信息交换码, American Standard Code for Information Interchange)

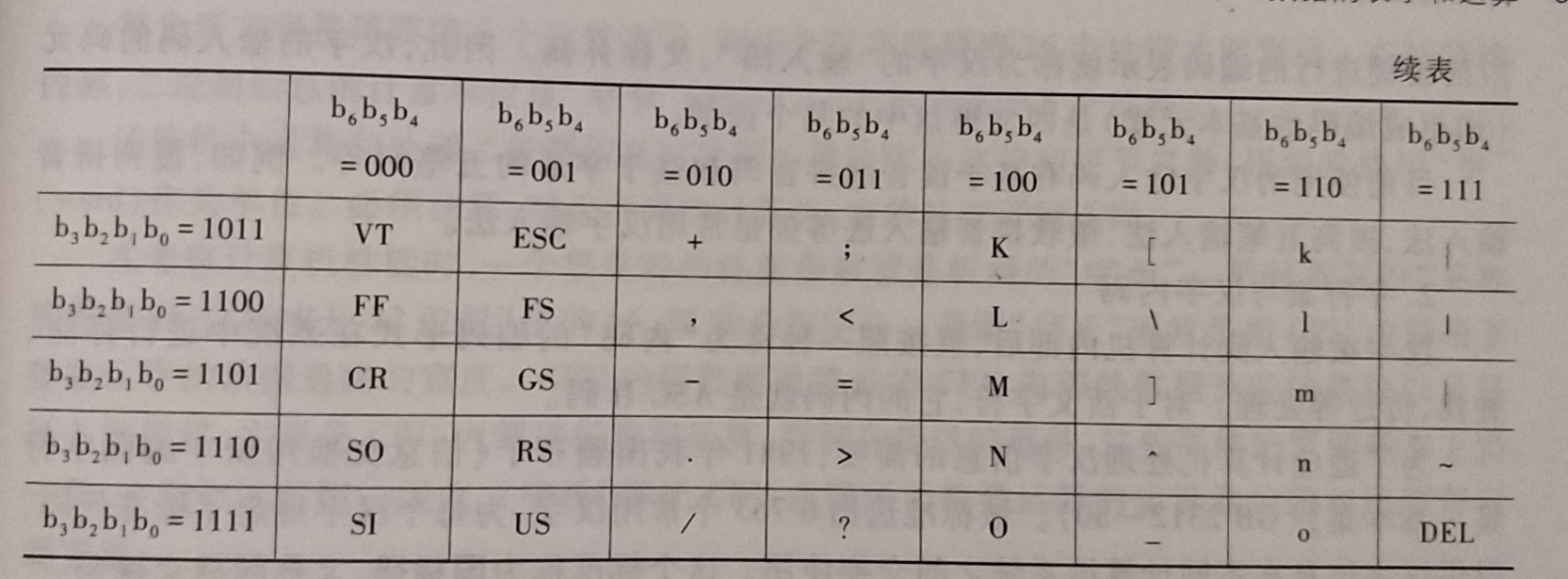
-
由上图可知, 每个字符由
7个二进制位\(b_6b_5b_4b_3b_2b_1b_0\)表示.- 其中 \( b_6b_5b_4是高位部分, b_3b_2b_1b_0是低位部分 \)
-
一个字符在计算机中实际用8位表示, 一般情况下最高一位\(b_7\)为0.
- 在需要奇偶校验时这一位存放奇偶校验值, 此时称为奇偶校验位
-
7个二进位从0000000到1111111共表示128种编码, 可表示128个不同字符
- 10个字符
- 26个小写字母
- 26个大写字母
- 算术运算符
- 标点符号
- 商业符号等
-
ASCII码有以下两个规律
- 字符0~9这10个数字字符的高三位编码为
011, 低4为分别为0000~1001. 去掉高三位时, 低4位正好是0~9这10个字符的8421码. 既满足了正常的排序关系, 又有利于实现ASCII码与十进制之间的转换 - 英文字母字符的编码值也满足字母排序关系. 大小写字母编码之间的差别在\( b_5 \)这位上, 若这位为0则是大写字母反之为小写字母.
- 字符0~9这10个数字字符的高三位编码为
2.4.3 汉字字符
- 西文字符仅用7-8位二进制即可表示.
- 汉字是表意文字, 一个字就是一个方块图形. 计算机要对汉字进行处理, 就必须对汉字本身进行编码.
- 为适应汉字系统各组成部分对汉字信息处理的不同需要, 汉字系统必须处理以下几种汉字代码
- 输入码
- 内码
- 字模点阵码
1. 汉字的输入码
- 专门的汉字输入键盘由于键多,查找不便,成本高等原因几乎无法使用
- 最简单, 最广泛采用的汉字输入方法是利用英文键盘输入汉字. (每个汉字用一个或多个键表示)
- 对每个汉字用相应的按键进行的编码表示就称为汉字的输入码, 又称外码.
- 汉字输入码的
码元(组成编码的基本元素)是西文键盘中的某个按键. - 目前的汉字输入码有基于拼音码和基于字形的五笔码等
- 搜狗拼音/搜狗五笔, 微软拼音输入法
2. 字符集和汉字内码
- 汉字输入到计算机内部后, 按照内码的编码形式在系统中进行存储查找/传送等处理.
- 西文字符的内码是
ASCII码
- 西文字符的内码是
- 1981年我国颁布《信息交换用汉字编码字符集·基本集》(GB2312-80), 又称为国标码, 又称为国标交换码
- 该标准选出6763个常用汉字, 为每个汉字规定了标准代码以供汉字信息在不同计算机系统之间交换使用
- GB2312字符集为任意一个字符(包括汉字和其他字符)规定了一个唯一的二进制代码.
- GB2312码表由94行(区号0~93), 94列(行号0~93)组成.
- 每个汉字或符号在码表有各自的位置(是一个唯一的位置编码), 称为区位码
区号和行号各占一个字节, 各自加上32(20H), 再将两个字节的最高位\(b_7\)置为"1”
- 以上双字节汉字编码是其中的一种汉字的内码
- 汉字的
区位码和国际码是唯一的,标准的, 而汉字的内码可能随系统的不同而有差别. - 国际标准
ISO/IEC 10646提出一种包括全世界现代书面语言文字所使用的所有字符的编码, 每个字符用4字节(UCS-4)或两个字节(UCS-2)进行编码.- 我国(包括香港台湾)与日本韩国联合制定了一个统一的汉字字符集(CJK编码), 收录了上述不同国家和地区的共约
2万多汉字及字符号, 采用UCS-2编码, 被批准为国家标准(GB 13000)
- 我国(包括香港台湾)与日本韩国联合制定了一个统一的汉字字符集(CJK编码), 收录了上述不同国家和地区的共约
- Windows操作系统(中文版)中也采用中西文统一编码, 称为Unicode(2字节编码), 与
ISO/IEC 10646的UCS-2编码一致
3. 汉字的字模点阵码和轮廓描述
- 汉字字形的主要描述方法有两种
- 字模点阵描述
- 将字库中的各个汉字或其他字符的字形(即字模), 用一个元素由0/1组成的方阵(16x16,32x32,64x64甚至更大)来表示, 汉字或字符中有黑点的地方用
1表示, 空白处用0表示 - 该种描述汉字字模的二进制点阵数据称为汉字的字模点阵码
- 轮廓描述
- 略微复杂. 把汉字的笔画的轮廓用一组直线和曲线来勾画, 记下每一直线和曲线的数学描述公式
- 目前已有两类国际标准 :
- Adobe Type1
- True Type
- 使用轮廓描述字形的方式精度高, 字形大小可随意变化
2.5 数据的宽度和存储
2.5.1 数据的宽度和单位
- 计算机内部所有信息都被表示成二进制编码形式
- 二进制数据的每一位(0或1)是组成二进制信息的最小单位, 称为一个比特(bit), 或者位元, 简称位
- 比特是计算机中处理/存储和传输信息的最小单位
- 每个西文字符需要8个比特表示,汉字需要16个比特表示
- 计算机内部二进制信息的计量单位是字节(byte), 一个字节等于8个比特
- 除比特和字节外, 还是用 字(word) 作为单位(不同计算机, 字的长度可能不一样)
- 字长 是考察计算机的重要性能参数(平时所说的32位机 64位机)
- 字长指的是 CPU内部用于
整数运算的数据通路的宽度- 内部数据通路指的是CPU内部的数据流经的路径以及路径上的部件
- 主要是CPU内部进行数据运算/存储/传送的部件, 要求这些部件的宽度基本上要一致才能相互匹配
- 字长等于CPU内部用于整数运算的运算器位数和通用寄存器宽度.
- 字长指的是 CPU内部用于
- 字和字长的概念不一样, “字"用来表示被处理信息的单位, 用于度量各种数据类型的宽度.
- Intel x86微处理器中把一个"字"定义成16位, 但从
80386微处理器开始, 字长至少是32位了. - 因此, 即使再一个字长为32位的计算机中, 32位也被称为双字宽
- Intel x86微处理器中把一个"字"定义成16位, 但从
- 存储容量的单位主要有
- \( 1KB=1024字节; 1MB=2^{20}字节; 1GB=2^{30}字节; 1TB=2^{40}字节; 1PB=2^{50}字节; 1EB=2^{60}字节; 1ZB=2^{70}字节; \)
- 描述距离,频率等数值时通常用10的幂次表示(由时钟频率计算得到的总线带宽或外设数据传输率中度量单位表示用的是10的幂次)
2.5.2 数据的存储和排序顺序
-
不同的数据类型具有不同的宽度.
-
以字节位一个排列基本单位, 则LSB(Least Significant Byte), 最低有效字节, MSB(Most Significant Byte), 最高有效字节
- 例如,数5再32位机器上用int类型表示时0/1序列为
0000 0000 0000 0000 0000 0000 0000 0101, 其中MSB=00H, LSB=05H
- 例如,数5再32位机器上用int类型表示时0/1序列为
-
字节编址方式 : 对存储空间的存储单元进行编号时, 每个地址编号放入一个字节
short: 2byteint/float: 4bytedouble: 8byte
-
数据的地址指的是其所占用若干个连续存储单元的地址中最小的地址(参考C语言中的数组类型)
- 例如 : 在一个按字节编码的计算机中, 假定int类型变量i的地址为
08 00H, i的机器数为01 23 45 67H, 则i所占的存储单元的地址为08 00H, 08 01H, 08 02H, 08 03H 08 00H, 08 01H, 08 02H, 08 03H应该是从大地址向小地址存放还是小地址向大地址存放, 这就是字节排列顺序问题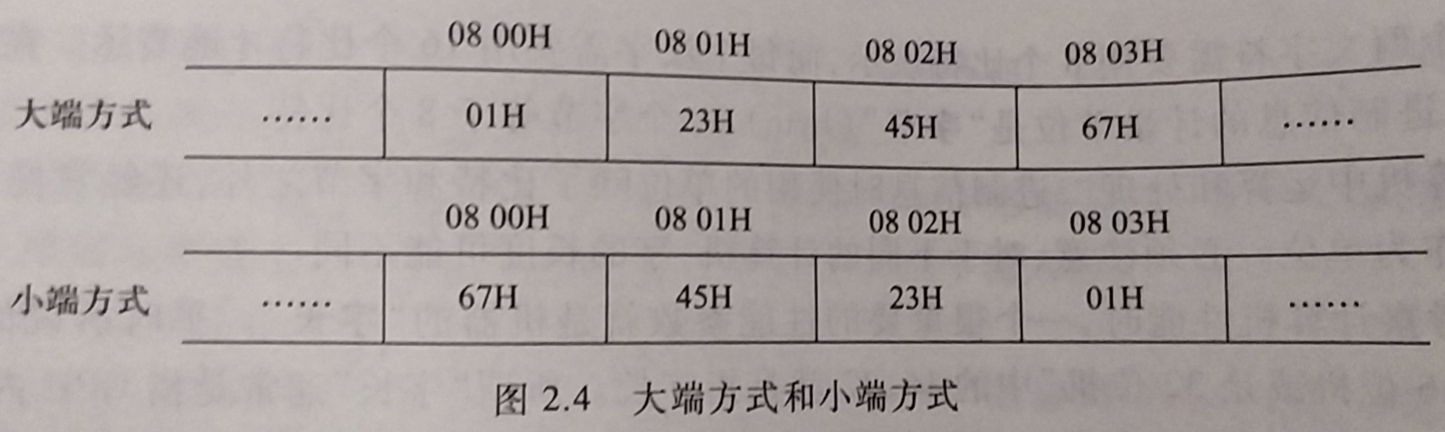
- 例如 : 在一个按字节编码的计算机中, 假定int类型变量i的地址为
-
数据各字节在连续存储单元中排列顺序的不同, 分为 大端和小端 两种排列顺序
- 大端(big endian) : 将数据的最高位有效字节 MSB 存放在最小地址单元中, 将最低位有效字节 LSB 存放在最大地址单元中, 即 数据的地址就是
MSB所在的地址- 例子中的变量i的MSB为 01H, LSB为67H
- IBM 360/370,Motorola 68k, MIPS, Sparc, HP PA等机器都使用大端方式
- 小端(little endian) : 将数据的最高位有效字节 MSB 存放在高地址单元中, 将最低位有效字节 LSB 存放在低地址单元中, 即 数据的地址就是
LSB所在的地址- Intel 80x86,DEC VAX等都采用小段方式
- 大端(big endian) : 将数据的最高位有效字节 MSB 存放在最小地址单元中, 将最低位有效字节 LSB 存放在最大地址单元中, 即 数据的地址就是
2.6 数据校验码
- 计算机内部在处理数据时, 可能由于元器件故障或噪音干扰等原因会出现差错.
- 要减少避免这些错误
- 需要从硬件本身的可靠性入手, 在电路/电源/布线等各方面采取必要措施, 提高计算机抗干扰能力
- 采取相应的数据检错和校正措施, 自动发现并纠正错误.
- 常用的数据校验
- 奇偶校验码
- 海明校验码
- 循环冗余校验码
2.6.1 奇偶校验
-
最简单的一种校验方法
-
实现原理 :
假设将数据 \( B=b_{n-1}b_{n-2}…b_1b_0 \) 从源部件发送到终部件, 在终部件接收到的数据为 \( B'=b_{n-1}‘b_{n-2}’…b_1’b_0' \)
如果要判断数据
B在传送中是否发生错误, 可用以下步骤进行判断- 在源部件求出奇(偶)校验位P.
- 若采用奇校验方式, 则 \( P=b_{n-1} \bigoplus b_{n-2} \bigoplus … \bigoplus b_1 \bigoplus b_0 \bigoplus 1 \), 当B中有奇数个1时, P取0反之取1
- 若采用偶校验方式, 则 \( P=b_{n-1} \bigoplus b_{n-2} \bigoplus … \bigoplus b_1 \bigoplus b_0 \), 当B中有偶数个1时, P取0反之取1
- 例如传送字符’A(ASCII码为 100 0001)', 编码中有两个1, 所以奇校验位P=1, 在前面增加奇校验位后的编码为 1 100 0001
- 若是采取偶校验方式, 则P=0, 前面增加偶校验位后的编码为 0 100 0001
- 在终部件求出奇(偶)校验位P'.
- 采用奇校验方式 : \( P'=b_{n-1}'\bigoplus b_{n-2}'\bigoplus …b_1'\bigoplus b_0'\bigoplus 1 \)
- 采用偶校验方式 : \( P'=b_{n-1}'\bigoplus b_{n-2}'\bigoplus …b_1'\bigoplus b_0' \)
- 上述例子假定传送的ASCII 100 0001被传送到终部件后, 变成了 100 0011, 则得到奇校验位P=0, 若是偶校验位则P=1
- 计算最终的校验位\( P^{*}\) , 并根据其值判断有奇偶错. P与B是一起从源部件传到终部件的, 假定P在终部件接收到的值为 \( P'', 则 P^*=P' \bigoplus P''. 若 P^*=1, 则表示有奇数位错; 若 P^*=0, 则表示正确或有偶数个错 \)
假定P被传送到终部件后没有发生变化, 即
$$
奇校验方式 P”=P=1, 或者偶校验方式 P”=P=0.
$$ $$ 那么, 奇校验方式下, P^*=P' \bigoplus P”=0 \bigoplus 1 = 1; 奇校验方式下, P^*=P' \bigoplus P"=1 \bigoplus 0 = 1 $$ 不管采用奇校验还是偶校验, 最终的 \( P^* 都等于1\), 说明有奇数位错(100 0001变成100 0011发生了一位出错)
- 在奇偶校验码中, 只能发现奇数位出错, 不能发现偶数位出错, 也不能确定发生错误的位置, 不具有纠错能力
- 但奇偶校验开销小, 常被用于存储器读写检查或按字节传输过程的数据校验
- 一字节长的代码中一位出错的概率相对较大, 两位以上出错则很少, 所以奇偶校验用于校验一字节长的代码还是很有效的.
- 在源部件求出奇(偶)校验位P.
-
奇偶校验是对所有数据生成一位校验位, 所以校验检错能力差, 且没有纠错能力
2.6.2 海明校验
-
海明校验码 由
Richard Hamming于1950年提出, 主要思想:- 将数据按某种规律分成若干组, 对每组进行相应的奇偶检测, 提供多位校验信息, 从而实现对错误位置进行定位, 并将其纠正
- 实质上就是一种多重奇偶校验码
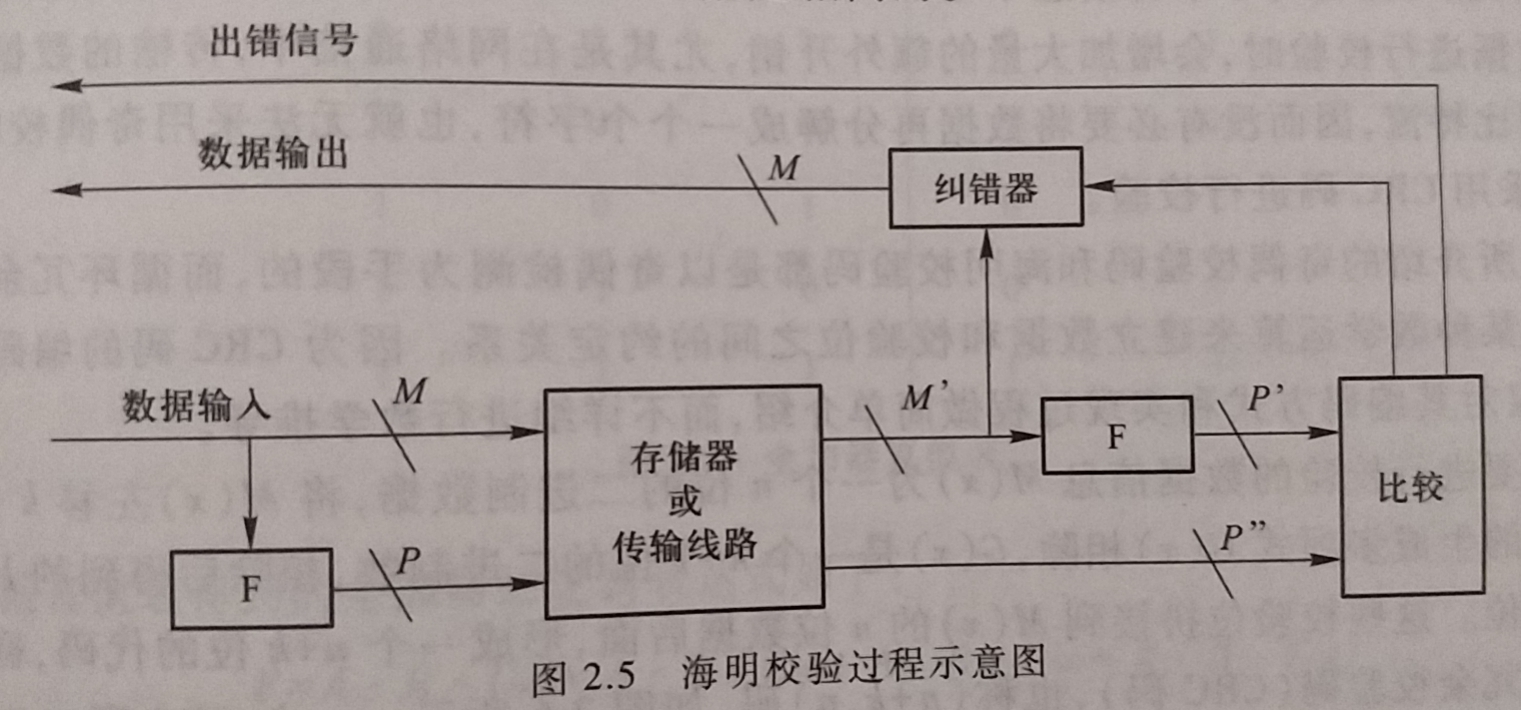
- 海明校验在最终比较时按位进行异或操作, 即P’和P"按位异或, 根据异或操作的结果, 确定是否出错.
- 异或操作所得结果被称为故障字(syndrome word)
- 校验位的位数的确定
- 假定被校验数据M的位数为n, 校验位P为k位, 则故障字的位数也为k位. 则k位的故障字可表示的状态最多为 \( 2^k种 \), 每种状态可用来说明一种出错情况
- 对于最多只有一位错的情况, 结果可能是无错或n位数据中的某位出错或k位校验码中某一位出错
- 因此共有1+n+k种情况, 所以要能对一位错的所有结果进行正确表示, 则n和k必须满足以下关系 $$ 2^k ≥ 1+n+k, 即 2^k-1 ≥ n+k $$
- 对于单个位纠错的情况, 当数据有8位时, 校验位和故障字都应有4位(最多可表示16种状态, 单个位出错情况最多只有12种可能(8个数据位和4个校验位中的某一位出错, 再加上无错的情况, 一共13种)).
- 分组方式的确定
- 数据位和校验位是一起被存储的, 通过将它们种的各位按某种方式排列位一个(n+k)位的码字, 将该码字种每位的出错位置与故障字的数值建立关系, 这样就可通过故障字的值很快确定是该码字种的哪位发生错误, 从而将其取反来进行纠正
- 根据上述基本思想, 可按照以下规则解释各故障字的值
- 故障字各位全部为0, 则没有发生错误
- 故障字中有且仅为一位为1, 则表示有一位出错, 不需要纠正
- 故障字中多位为1, 则表示有一个数据位出错, 其在码字中的出错位置由故障字来确定, 纠正时只要将出错位取反即可
- 海明校验有 单纠错码(SEC) 和 单纠错/双检错码(SEC-DED)
- 前者只能对单个位出错进行定位和纠错
- 后者同时具有发现两位错和纠正一位错的能力, 称 纠一检二码
2.6.3 循环冗余校验
- 循环冗余校验码(Cycle Redundancy Check), 简称CRC码, 具有较强检错/纠错能力的校验码, 多用于外存储器的数据校验, 计算机通信中也广泛使用.
- 数据传输中, 奇偶校验码是在每个字符信息中增加一个奇偶校验位, 这样对大批量传输的数据校验时会增加大量额外开销, 尤其是网络通信中, 传输的数据都是二进制比特流, 因而没有必要将数据再分解成一个个字符, 也就无法采用奇偶校验码, 因此通常采用CRC校验码
奇偶校验码和海明校验码都是以奇偶检测为手段的- 而循环冗余校验码则是通过某种数学运算来建立数据和校验位之间的约定关系(很复杂,书本只做简单介绍,没有进行数学推导, @Todo)
- 假设要进行校验的数据信息M(x)是一个n位的二进制数据, 将M(x)左移k位后, 用一个约定的生成多项式G(x)相除, G(x)是一个k+1位的二进制数, 相除后得到的k位余数就是校验位
- 将校验位拼接到M(x)的n位数据后, 形成一个 n+k 位的代码, 称这个代码为
循环冗余校验码(CRC码), 也称(n+k,n)码 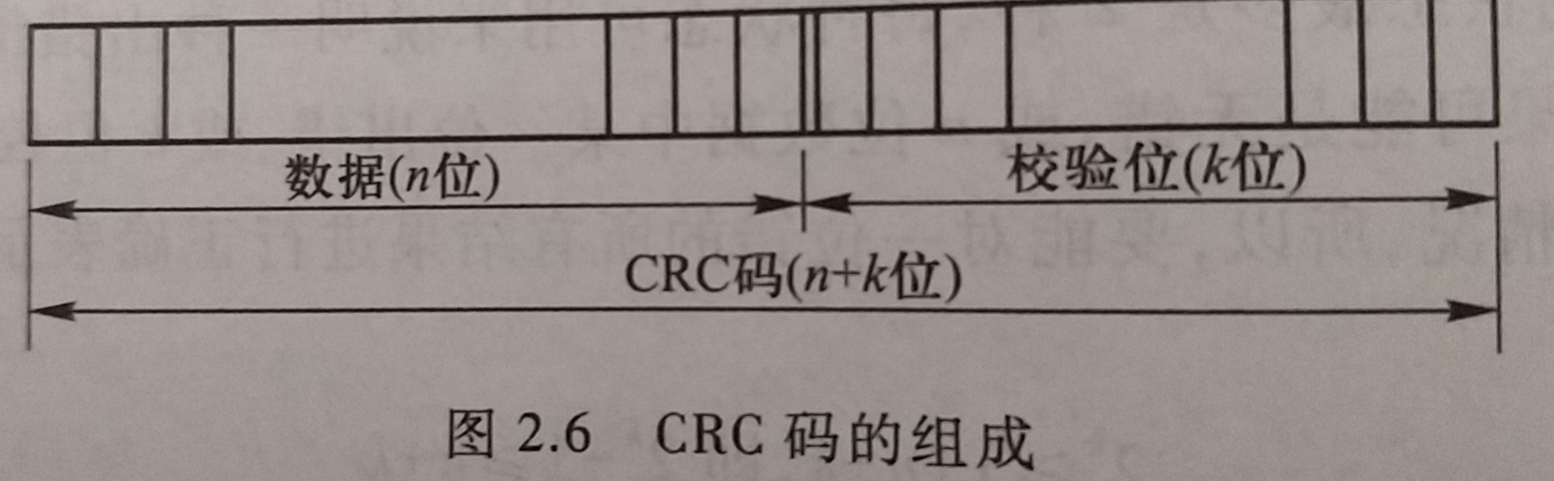
- 一个CRC码一定能被生成多项式整除, 故当数据和校验位一起送到接收端后, 只要将接收到的数据和校验码用同样的生成多项式相除, 如果正好除尽, 则没有发生错误;若除不尽, 则表明某些数据位发生了错误
网络通信知识点
- 网络通信中, 通常n相当大, 由几千个二进位构成一帧数据, 因此通常使用CRC码来检测错误, 发现错误则告知发送方要求重发, 不用CRC来纠正错误.
- 因此只要在接收方用约定的生成多项式进行模2除后判断余数是否为0就行了
2.7 加法器和算术逻辑部件
- 一般情况下用一个专门的 算术逻辑部件(Arithmetic and Logic Unit, ALU) 来完成基本逻辑运算和定点数加减运算, 各类定点乘除运算和浮点数运算可利用加法器或ALU和移位器实现
- 因此基本的运算部件是
加法器,ALU和移位器,ALU的核心部件是 加法器.
2.7.1 全加器和加法器
-
全加器(Full Adder, FA) : 同时考虑两个加数和地位进位的
一位加法器- 全加器两个加数为
A和B, 低位进位为Cin, 相加的和为F, 向高位的进位为Count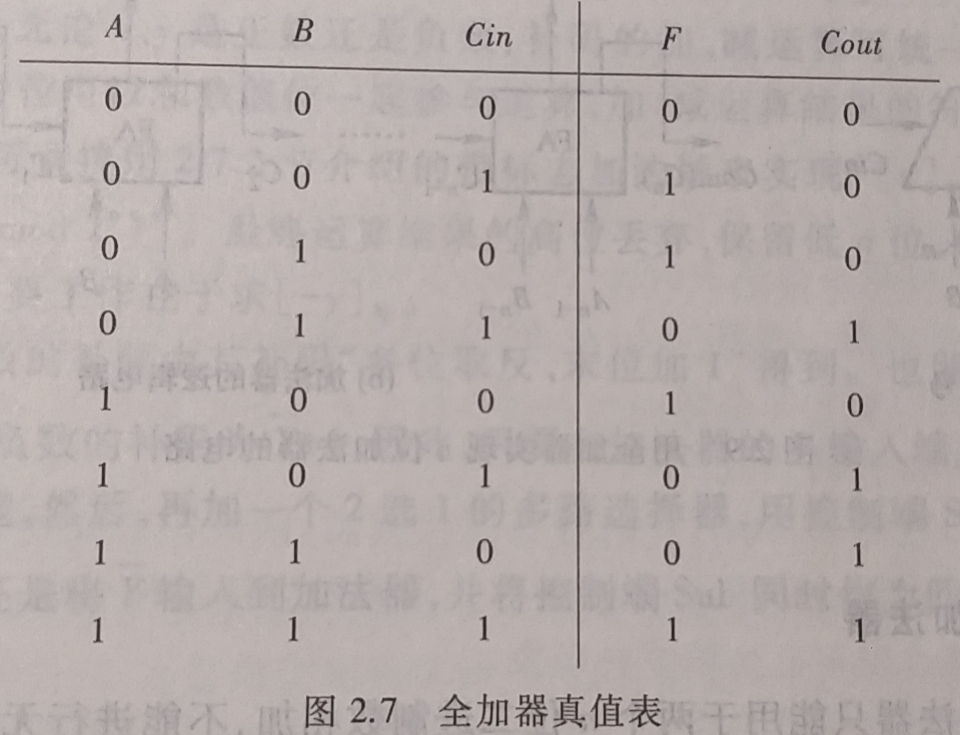
- 全加器两个加数为
-
根据上图真值表得到的全加器 逻辑表达式 如下 : $$ F = \overline{A} · \overline{B} · Cin + \overline{A} · B · \overline{Cin} + A · \overline{B} · \overline{Cin} + A · B · Cin $$ $$ Count = \overline{A} · B · Cin + A · \overline{B} · Cin + A · B · \overline{Cin} + A · B · Cin $$
- 符号解析 : \( \overline{A}指的是A的值取反, 也是逻辑非的意思; A · B按照目前套公式结果都相同的情况下得出两种意思 : 第一种是逻辑与, 第二种是 A*B的意思 \)
-
使用
布尔代数定律对上述逻辑表达式简化后得到 全加和F 和 全加进位Count 的逻辑表达式为 $$ F=A \bigoplus B \bigoplus Cin $$ $$ A · B + A · Cin + B · Cin $$ -
根据全加器逻辑表达式, 得到全加器逻辑电路如下图
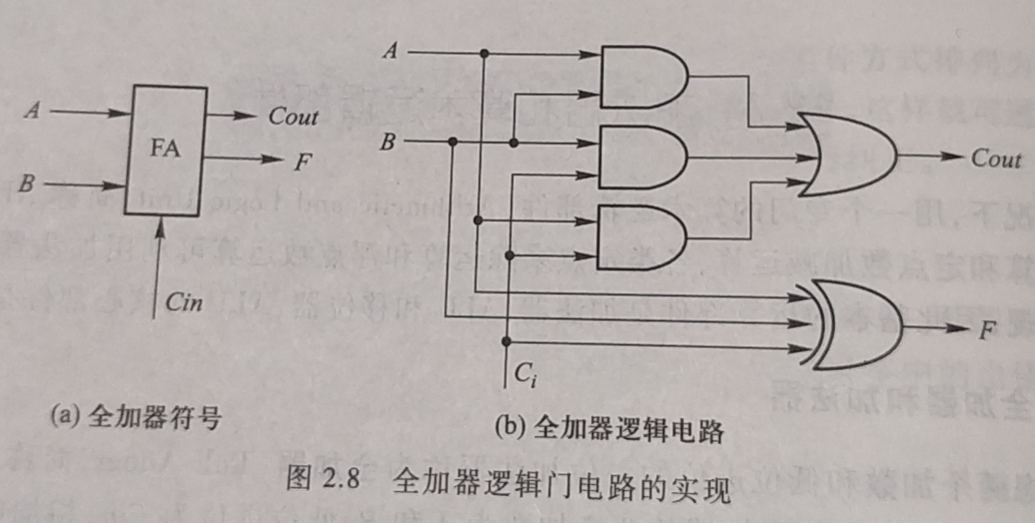
-
加法器 又称 无符号加法器. n位加法器可由n个全加器实现(电路如下图,a是符号表示, b给出全加器构成加法器的实现电路,\( C_i是第i-1位向第i位的进位 \))
-
全加器实现n位加法器, 使用的是 串行进位 , 速度很慢. (也可采用先行进位方式的各类先行加法器等)
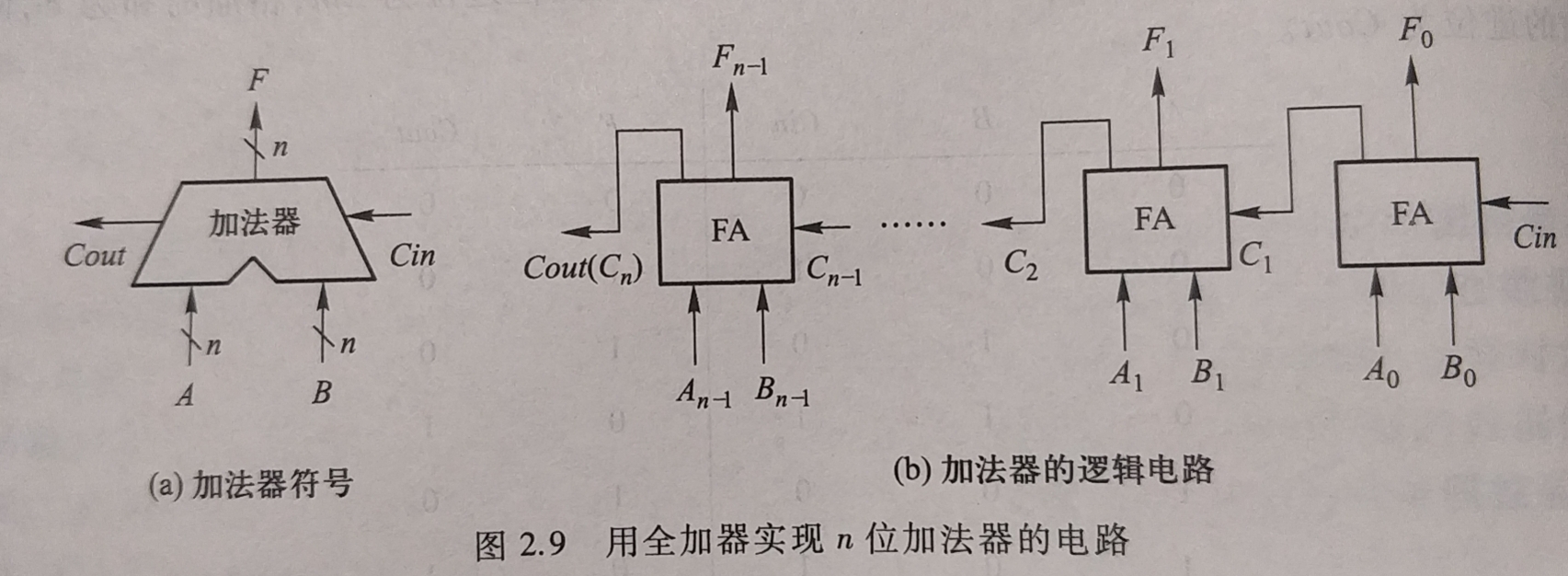
2.7.2 带标志加法器
-
n位无符号的加法器只能计算n位二进制的相加, 不能计算无符号整数的相减, 也不能对有符号整数进行加减.
-
需要在无符号加法器的基础上增加相应的逻辑门电路才能完成以上需求. (不仅能计算结果, 还能生成相应的标志信息)
-
下图是带标志加法器实现电路的示意图, a是符号表示, b给出用全加器构成的实现电路
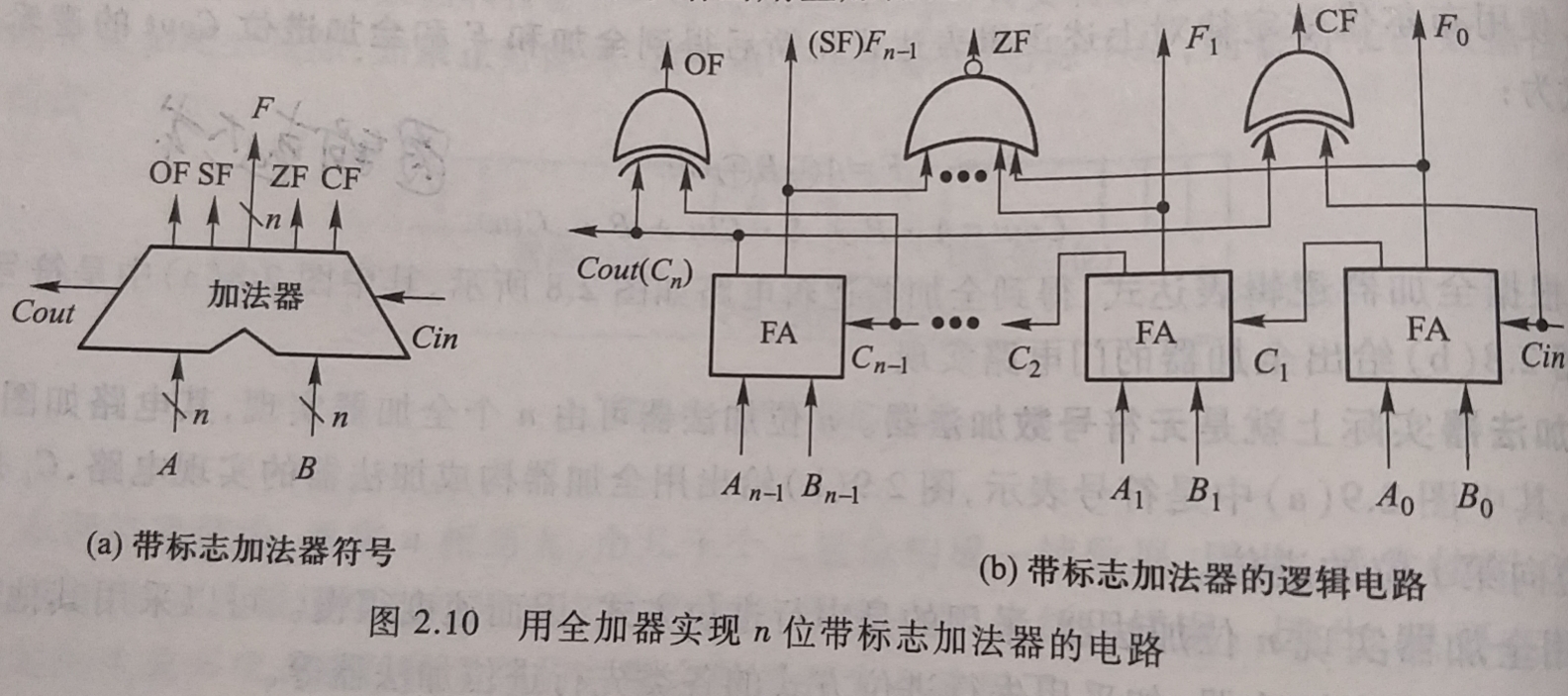
-
上图所示的
溢出标志的逻辑表达式为 \( OF=C_n \bigoplus C_{n-1} \); 符号标志就是和的符号, 即 \( SF=F_{n-1} \) -
零标志ZF=1当且仅当F=0时; 进位/借位标志 \( CF=Count \bigoplus Cin, 当Cin=0时,CF为进位Count, 当Cin-1时, CF为进位Count取反 \)
-
为了加快加法运算的速度, 真正的电路一定是使用多级先行进位方式; 上图主要是为了说明如何从加法运算结果中获得标志信息, 因为使用全加器以简化加法器电路
2.7.3 补码加减运算器
-
若 \( x_{补}=X=X_{n-1}X_{n-2}X_1X_0,y_补=Y=Y_{n-1}Y_{n-2}Y_1Y_0, 则 (x+y)_补和(x-y)_补 的运算表达式可以简化为 \) $$ (x+y)_补 = x_补 + y_补 (mod 2^n) $$ $$ (x-y)_补 = x_补 + -y_补 (mod 2^n) $$
-
无论x,y是正数还是负数, 补码的加减运算可统一用加法实现, 且x,y的补码的符号位可以和数值位一起参与运算, 加减运算结果的符号位也在求和运算中得出.
-
可用带标志加法器实现上面两条表达式, 最终运算结果的高位丢弃, 保留低n位, 相当于对和取模\( 2^n \)
-
因此, 实现减法的主要工作在于求 -y 的补码
-
一个数的负数的补码由其补码 各位取反, 末位加1.
- 要得到一个已知数的补码表示为
Y, 则该数的负数的补码则为 \( \overline{Y}+1 \)
- 要得到一个已知数的补码表示为
-
在加法器中实现减法
- 只要在加法器的Y输入端加n个反向器, 就可实现各位取反的功能, 再加一个 2选1 的多路选择器, 用控制端Sub来控制选择将原码Y输入到加法器还是将 \( \overline{Y} \)输入到加法器, 并将控制端Sub同时作为低位进位送到加法器
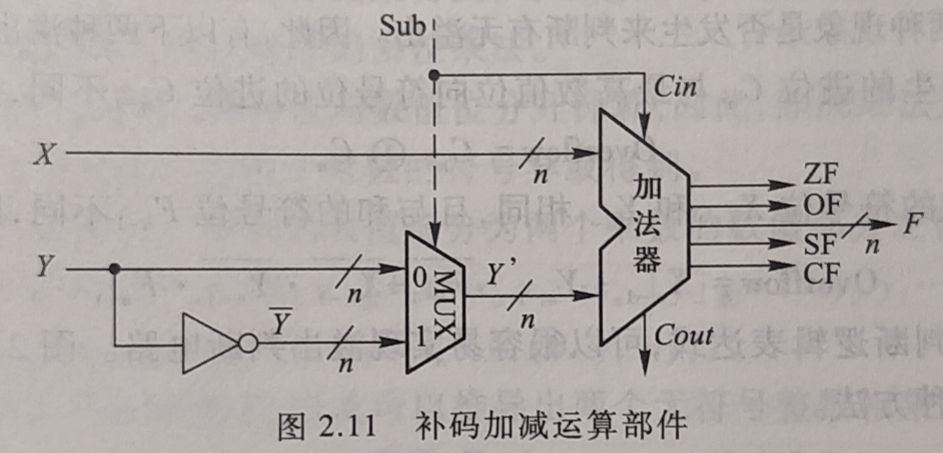
- 该电路可实现补码加减运算
- Sub为1, 减法运算, 实现 \( X+\overline{Y}+1 = x_补+-y_补 \)
- Sub为0, 加法运算, 实现 \( X+Y = x_补+y_补 \)
-
无符号整数相当于正整数, 正整数的补码表示等于其二进制表示本身. 因此该电路同时也能实现无符号整数的加减运算
-
通过标志信息区分带符号整数运算结果和无符号整数运算结果
- 零标志ZF=1表示结果F为0, 不管作为无符号还是带符号整数来运算, ZF都有意义
- 符号标志SF表示结果的符号, 即F的最高位. 对于无符号运算, SF没有意义.
- 进位/借位CF表示无符号数加减运算时的进位与借位
- 加法时, 若CF=1表示无符号数加法溢出. 做加法时, CF就应等于进位输出Count
- 减法时, 若CF=1表示由借位,不够减, 做减法时, 应将进位输出Count取反作为借位标志
- 综合可得 \( CF=Sub \bigoplus Count \)
- 对于带符号整数运算, CF没意义
-
对于n位补码整数, 可表示的数值范围为 \( -2^{n-1} ~ (2^{n-1}-1) \); 当运算结果超出该范围则结果溢出.
-
补码溢出判断方法如下:
用4位补码计算 "-7-6"和"-3-5"的值
-7的补码等于0111取反后加1等于1001
-6的补码等于0110取反后加1等于1010
-3的补码等于0011取反后加1等于1101
-5的补码等于0101取反后加1等于1011
[-7-6]=1001+1010=0011(+3)
[-3-5]=1101+1011=1000(-8)
4位补码可表示范围为 -8 ~ +7. 而-7-6=-13, -13<-8, 所以结果0011(+3)一定发生了溢出, 是一个错误的值
经-7-6发现两个现象:(如下图)
1. 最高位和次高位的进位不同
2. 和的符号位和加数的符号位不同
而-3-5结果为1000(-8), 没有超出范围且没有发生溢出, 是一个正确的值,
且最高位和次高位的进位都是1, 没有发生上面的第1种现象, 且和的符号位和加数的符号都是1, 也没有发生上面的第2种现象.
- 通常根据上述两种现象是否发生来判断有无溢出, 因此得出两种溢出判断逻辑表达式
- 若符号位产生的进位 \( C_n 与最高数值位向符号位的进位 C_{n-1}不同,则产生溢出, 即 Overflow=C_{n-1}\bigoplus C_n\)
- 若两个加数的符号位 \( X_{n-1}和Y_{n-1}相同,且与和的符号位F_{n-1}不同,则产生溢出, 即 Overflow=X_{n-1} · Y_{n-1} · \overline{F_{n-1}} + \overline{X_{n-1}}·\overline{Y_{n-1}} · F_{n-1} \)
- 根据上述溢出判断逻辑表达式, 可以很容易实现溢出判断电路

2.7.4 算术逻辑部件
-
算术逻辑部件ALU是一种能进行多种算术运算与逻辑运算的组合逻辑电路, 其
核心部件是 带标志加法器, 多采用 先行进位方式 -
ALU所示图中,
- A和B是两个n位操作数输入端
- Cin是进位输入端
- ALUop是操作控制端, 用来决定ALU所执行的处理功能(选择add运算,ALU就执行加法运算,输出结果是A+B的和)
- ALUop的位数决定了操作的种类(当位数为3位时, ALU最多只有8种操作)
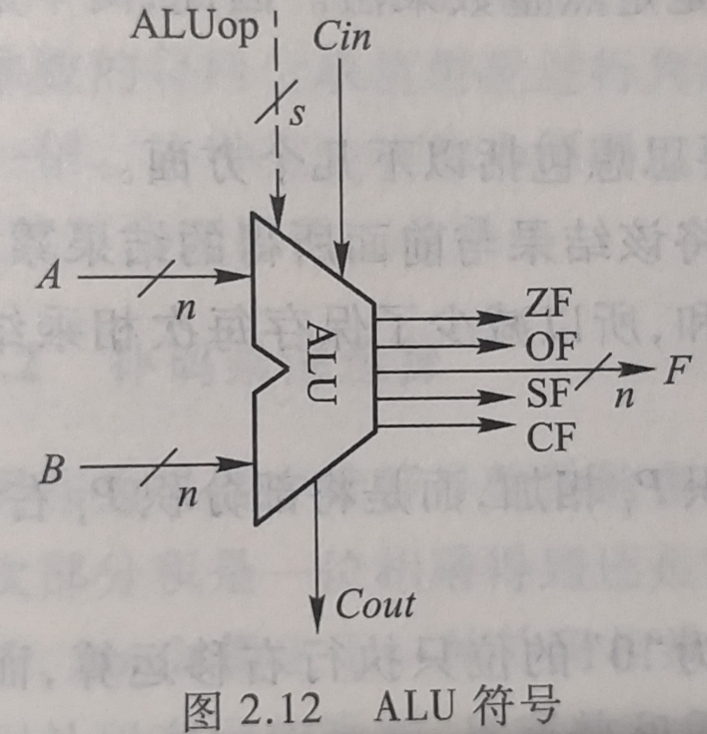
- ALUop的位数决定了操作的种类(当位数为3位时, ALU最多只有8种操作)
-
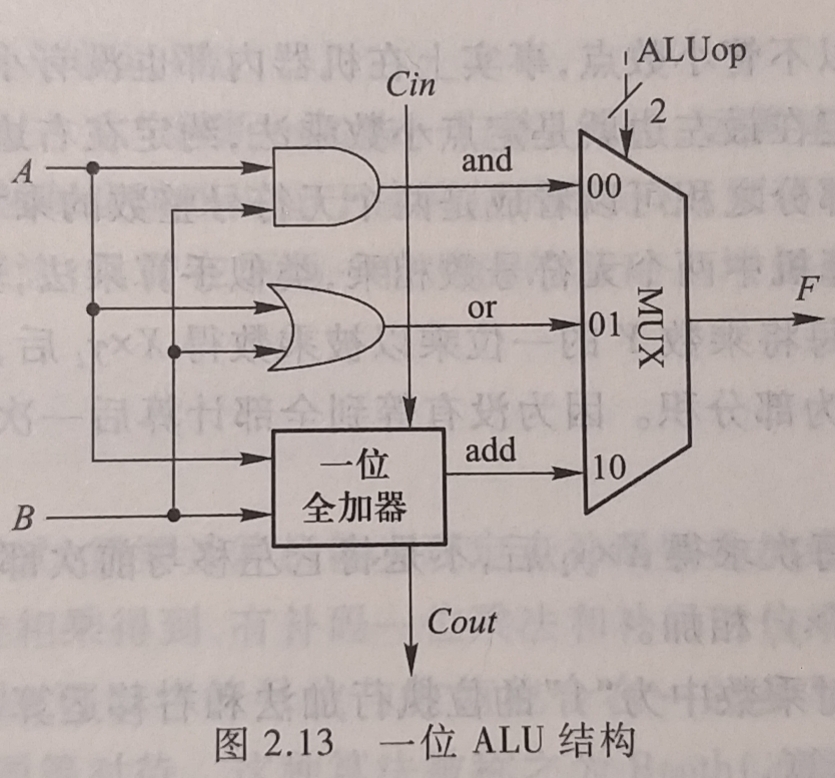
一位ALU结构中
- 能完成三种运算, 与/或/加法
- 一位加法使用一个全加器实现, 在ALUop控制下, 由一个多路选择器(MUX)选择输出三种操作之一
- 有三种操作, ALUop至少要有两位
2.8 定点乘法运算
- 乘法器 在
图像/语音/加密等数字信号处理领域扮演者重要的角色, 且很大程度决定系统性能, 也是处理器中的关键部件, 程序中的运算大约三分之一是乘法运算. - 乘法器有带符号整数乘运算所用的补码乘法器和无符号整数或浮点数尾数相乘所用的无符号乘法器
- 原码乘法运算在无符号乘法器的基础上实现
2.8.1 原码乘法运算 (看不懂运算过程, 有空找一下相关资料)
-
原码作为浮点数尾数的表示方式, 需要计算机能实现定点原码小数的乘运算
-
根据每次部分积是一位相乘得到还是两位相乘得到, 可以有
- 原码一位乘法
- 原码两位乘法
- 根据原码两位乘法的原理推广, 可以有原码多位乘法
-
原码实现乘法运算, 符号位与数值位分开计算
- 确定乘积的符号位, 由两个乘数的符号
异或得到 - 计算乘积的数值位, 数值部分为两个成熟的数值部分之积
- 确定乘积的符号位, 由两个乘数的符号
-
原码乘法算法如下:
- \( 已知 x_原=X=x_0·x_1·x_2·…x_n, y_原=Y=y_0·y_1·y_2·…y_n, 则x×y_原=z_0·z_1·…z_{2n} \)
- \(其中z_0=x_0\bigoplus y_0, z_1…z_{2n}=(0.x_1…x_n)(0.y_1…y_n)\)
-
以下一个手算乘法的例子, 可推导出两个无符号整数相乘的计算过程.

-
可以不理会小数点, 事实上, 在机器内部也没有小数点, 只是
约定了一个小数点的位置, 约定在最左边(0的后一位)就是 定点小数乘法; 约定在最右边就是 定点整数乘法- 两个定点小数的数值部分的乘积可看作是两个无符号整数的乘积
-
无符号相乘, 类似手算乘法, 主要步骤 :
- 每次将
乘数Y乘以被乘数X得到 \( X×y_i后, \) 就将该结果与前面所得的结果累加,- 得到 \( P_i \), 称为 部分积. 因为没有等到全部计算后一次求和, 所以减少了保存每次相乘的结果的开销
- 每次求得\( X×y_i的乘积后, 不是将左移与前面部分积 P_i相加, 而是将部分积 P_i右移一位, 然后与该次结果相加(记住手算乘法) \)
- 对乘数中为1的位执行加法和右移运算,为0的位
只执行右移运算而不需要执行加法运算.- 因为每次执行加法运算, 只需要将 \( X×y_i \) 与部分积中的高n位进行相加, 低n位不会改变, 因此只需用n位加法器就可实现两个n位数相乘
- 每次将
-
实现上述的算法, 需要对乘数Y的每一位进行迭代得到相应的部分积\( P_i \)
- 取乘数的最低位 \( y_{n-i} \)判断
- 若\( y_{n-i}的值为1, 则将上一步迭代得到的部分积 P_i与X相加; 若为0, 则什么也不做 \)
- 右移一位, 产生本次部分积 \( P_i \)
- 部分积与X进行无符号整数相加时, 可能会产生进位, 因而需要一个专门的进位位C. 迭代过程从乘数最低位\( y_0和P_0=0开始, 经过n次"判断->加法->右移"循环, 直到求出P_n为止(最终乘积). \)
-
求\( x_原=0.1101, y_原=0.1011, 用原码一位乘法计算两者乘积的原码 \)
- 解: 先采用无符号乘法计算 1101×1011的乘积, 原码一位乘法过程如下
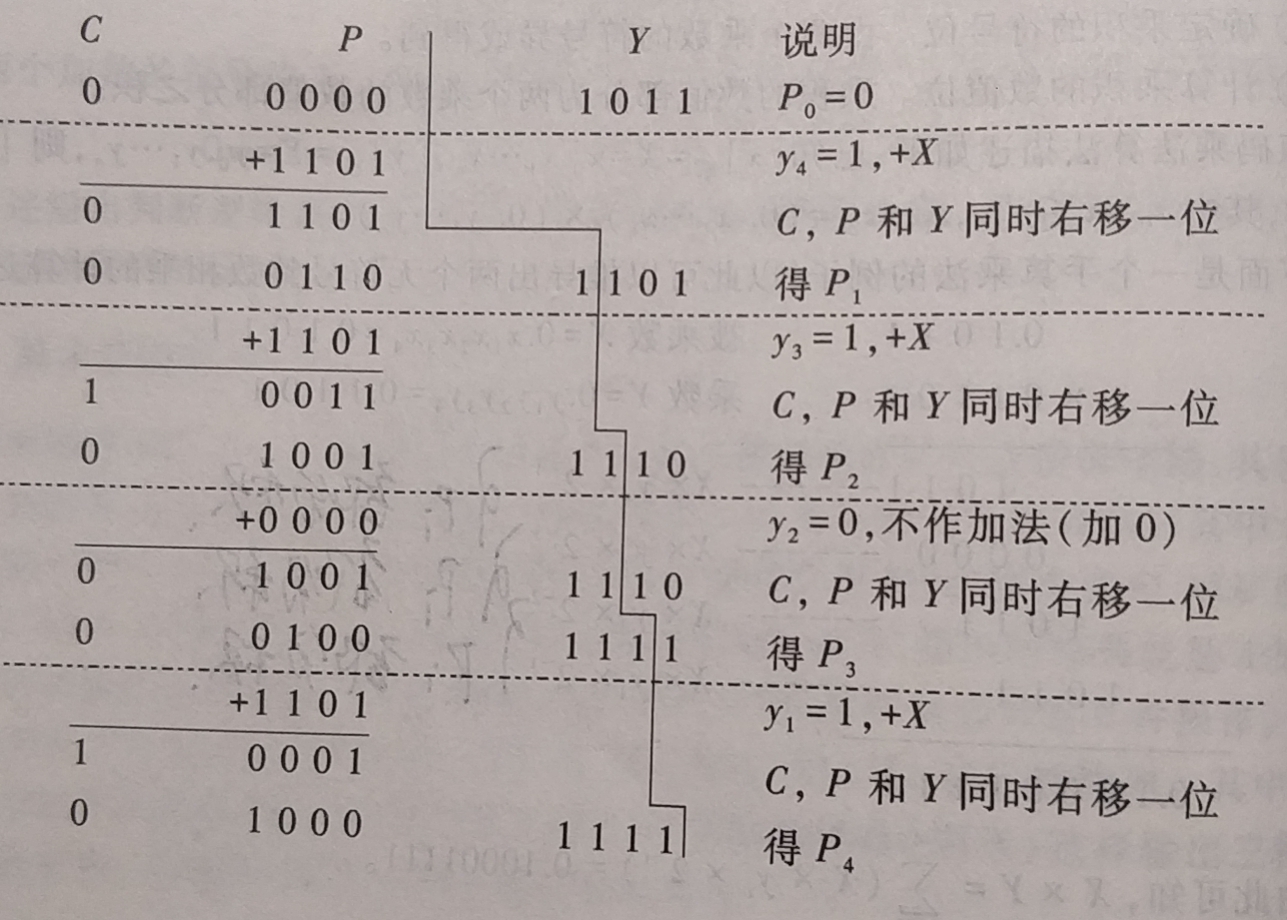
- 符号位为 \( 0 \bigoplus 0=0 \), 所以结果为 0.10001111
-
原码一位乘法运算速度慢. 如果对乘数的每两位取值情况进行判断, 每步求出对应于该两位的部分积, 可将乘法速度提高一倍, 称为 原码二位乘法
- 只需在原码一位乘法的基础上增加少量的逻辑线路, 就可实现
2.8.2 补码乘法运算 (看不懂运算过程, 有空找一下资料)
- 补码作为机器中带符号整数的表示形式, 需要计算机能实现定点补码整数的乘法运算.
- 根据每次部分积是一位相乘得到还是两位相乘得到, 补码也有补码一位乘法和补码两位乘法
- Booth(布斯)乘法 : 由
A.D.Booth提出的一种补码相乘算法, 可将符号位与数值位合在一起参与运算, 得出用补码表示的乘积, 且正负数同等对待 - 整数运算参与运算的数据都是字节的整数倍, 只需要考察偶数位的补码定点整数的乘法运算
- 设n为偶数, \( x_补=X=x_{n-1}…x_1x_0 = Y =y_{n-1}…y_1y_0, 得到x×y_补的Booth乘法运算规则如下: \)
- 乘数最低位增加一位辅助位\( y_{-1}=0 \)
- 若\( y_iy_{i-1}=01,则+[x]_补;若是为10, 则+[-x]_补 \)
- 算术右移一位, 得到部分积
- 重复第二步和第三步n次, 得出结果 \([x×y]_补\)
`例子` : 已知x的补码=1101, y的补码为0110, 要求使用布斯乘法计算x乘以y的补码
-x的补码为0011, 布斯乘法过程如下图
根据途中的运算过程, x乘以y的补码结果为 1110 1110
验证 : x=-011B=-3, y=+110B=6, x乘以y=-0001 0010B=-18, 结果正确

- 布斯乘法的算法过程为n次"判断->加减->右移"循环, 在布斯乘法中, 遇到连续的1或连续的0时,可跳过加法运算直接进行右移操作, 因此效率较高
- 补码乘法也可以采用两位一乘的方法, 把乘数分成两位一组, 根据两位代码的组合决定加或减被乘数的倍数, 形成的部分积每次右移两位, 总循环次数为n/2.
- 该算法可将部分积的数目压缩一般, 从而提高运算速度
2.9 定点除法运算
- 进行定点除法运算前要对
被除数和除数的 取值和大小 进行判断以确定除数是否为0商是否为0是否溢出. 通常判断操作如下- 若
被除数为0,除数不为0, 或者定点整数除法时, |被除数| < |除数|(绝对值), 则说明商为0, 余数为被除数, 不再继续执行 - 若
被除数不为0,除数为0, 对于整数会发生"除数为0"异常; 对于浮点数则结果为 无穷大 - 若
被除数和除数都为0, 对于整数则发生除法错异常; 对于浮点数则有些机器产生一个不发信号的 NaN,即 quiet NaN
- 若
- 只有当
被除数和除数同时不为0且商也不可能溢出(例如补码中最大负数除以-1时会发生溢出)时, 才进一步进行除法运算
2.9.1 原码除法运算
- 原码作为
浮点数尾数的表示形式, 需要计算机能实现定点原码小数的除法运算. 除法运算与乘法运算相似, 都是一种移位和加减运算的迭代过程, 但比乘法运算更加复杂.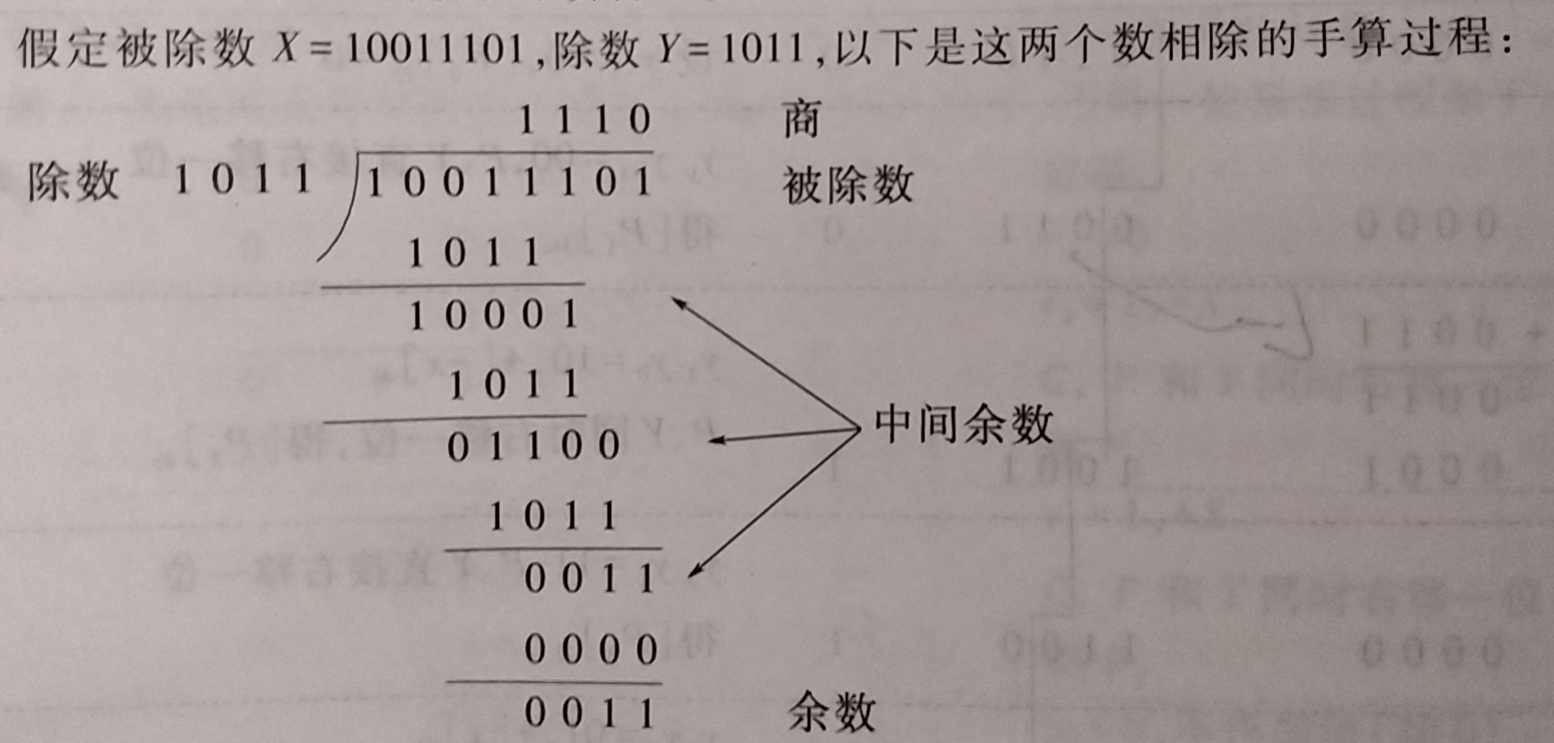
- 手算除法的基本要点 :
- 被除数与除数相减, 若够减则上商为1; 若不够上商为0
- 每次得到的差为中间余数, 将除数右移后与上次中间余数比较; 用中间余数减除数, 够减上商1否则上商0
- 重复执行第二步, 直到求得的商的位数足够为止
- 计算机内部的除法运算与手算算法一样, 通过
被除数(中间余数)减除数得到每一位的商 - 原码除法需要将符号位与数值位分开处理, 商的符号为相除两数符号的
异或值, 商的数值为两数的绝对值之商. - 因此要考虑定点正整数和定点正小数的除法运算
- 两个
32位数相除必须把被除数扩展成一个64位数. 因此得知, n位定点数的除法是用一个2n位的数去除以一个n位数, 得到一个n位的商- 因此需要进行被除数的扩展
- 定点正整数和定点正小数的除法运算的除法逻辑一样, 但是被除数的扩展方法不太一样, 此外导致溢出的情况也不一样
- (太难了, 略过了, 过后找别的资料进行学习吧)
2.9.2 补码除法运算
- 补码作为带符号整数的表示形式, 需要计算机能实现补码的除法运算
- 补码除法可将符号为与数值位合在一起进行运算, 且商的符号位直接在除法运算中产生
- 对于两个n位补码除法, 被除数需要进行符号扩展; 若被除数为2n位除数为n位则被除数无需扩展
- 在相除前同样需要对被除数与除数的取值和大小进行判断, 以确定除数是否为0,商是否为0,是否溢出
- (需要有原码除法运算基础, 过后找资料学习)
2.10 浮点数运算
2.10.1 浮点数加减运算
- 先理解一个十进制加法运算的例子,这也是可以看出浮点数加减法的运算规则; \( 0.123x19^5+0.456x10^2 \), 在此例子中不可以将0.123与0.456直接相加, 因为两者的指数不同, 要进行相加要先将两者的指数调整相等才可相加.计算过程如下
- \( 0.123x10^5+0.456x10^2 = 0.123x10^5+0.000456x10^5 \)
- = \((0.123+0.000456) x10^5 \)
- = \(0.123456x 10^5 \)
- 设两个规格化浮点数x和y表示为\( x=M_x×2^{E_x},y=M_y×2^{E_y}, 其中M_x,M_y分别是浮点数x和y的尾数,E_x,E_y分别是浮点数x和y的阶, 不失一般性,设E_x≤E_y,则 \)
- $$ x+y=(M_x×2^{E_x-E_y}+M_y)×2^{E_y} $$
- $$ x-y=(M_x×2^{E_x-E_y}-M_y)×2^{E_y} $$
- 而计算机中实现上述计算过程需要经过 对阶,尾数加减,规格化和舍入 四个步骤, 还需要考虑溢出判断和溢出处理问题(假定下面的讨论中 x±y 未经规格化的结果表示为 \( M_b×2^{E_b} \))
- 对阶
- 对阶的目的是为了x和y的阶码相等, 让尾数可以相加减. 对阶的原则是: 小阶向大阶看齐, 阶小的数的尾数向右移,右移的尾数等于两个阶的差的绝对值
- 举例 : \( 0.123×10^5+0.456×10^7 : 阶小的(5)向阶大的(7)看齐,阶小的尾数(0.123)右移, 右移的位数是两阶的差的绝对值(7-5), 得出0.00123×10^7+0.456×10^7 \)
- 大多数机器用IEEE754标准表示浮点数, 因此对阶时需进行移码减法运算且尾数右移时按原码小数方式右移, 符号为不参与移位, 数值位要将隐含的一位"1"右移到小数部分, 空出补"0"
- 为了保证运算的精准,尾数右移时,低位移出的位不要丢掉,应保留并参加尾数部分的运算.
- 根据补码的定义和IEEE754标准中阶码的定义, 可知
- $$ [\Delta E]_补 = [E_x-E_y]_补 = 2^n+E_x-E_y $$
- $$ = (2^{n-1}-1+E_x)+(2^n-(2^{n-1}-1+E_y)) $$
- $$ = [E_x]_移+[-[E_y]_移]_补(mod 2^n) $$
- $$ 其中[E_x]_移和[E_y]_移分别是阶E_x和E_y的阶码. $$
- 根据上述公式可知, 对阶时, 只要先对\( [E_y]_移求补,再与[E_x]_移相加, 就可以计算出[\Delta E]_补 \)
- 对阶码\( [E_y]_移求补时采用"各位取反末位加1"即可, 最后可根据 [\Delta E]_补的符号,判断出 \Delta E >0 还是 \Delta E ≤0 \)
- 对阶的目的是为了x和y的阶码相等, 让尾数可以相加减. 对阶的原则是: 小阶向大阶看齐, 阶小的数的尾数向右移,右移的尾数等于两个阶的差的绝对值
- 尾数加减
- 对阶后两个浮点数的阶码相等,此时可进行对阶后的尾数相加减.因为IEEE754标准采用定点原码小数表示尾数,所以尾数相加减实际是定点原码小数的加减.
- IEEE754浮点数尾数有一个隐藏位, 进行尾数加减时需要把隐藏位还原到尾数部分
- 对阶过程中, 尾数右移时保留的附加位也要参加运算
- 在用定点原码小数进行尾数加减时, 在操作数的高位部分和低位部分需要进行相应的调整
- 加减后的尾数不一定是规格化的, 所以浮点数的加减运算需要进一步规格化处理
- 尾数规格化
- IEEE754的规格化尾数形式为 : ±1.bb…b.
- 尾数加减后可能会得到不同形式的结果
- 1.bbb…bb + 1.bbb…b = ±1b.bb…b
- 1.bbb…bb - 1.bbb…b = ±0.00…1b…b
- 对于上述第一种情况需要进行 右规 : 尾数右移一位,阶码加1.
- 右规操作可以表示为 : \( M_b⬅M_b×2^{-1},E_b⬅E_b+1 \)
- 尾数右移时最高位'1’被移到小数点前一位作为隐藏位,最后一位移出时要考虑舍入
- 阶码加1时直接在末位加1
- 对于上述第二种情况需要进行 左规 : 数值位逐次左移,阶码逐次减1,直到将第一位'1’移到小数点左边.
- 假定结果中±和最左边的第一个1之间连续0的个数为k, 则左规操作可表示为 : \( M_b⬅M_b×2^k,E_b⬅E_b-k \)
- 尾数左移时数值部分最左边k个0被移出,所以小数点右移了k位.
- 尾数相加时, 默认小数点位置在第一个数值位(隐藏位)之后, 所以小数点右移k位后被移到了第一位1后面(隐藏位)
- 执行\( E_b⬅E_b-k \)时,每次都在末位减1, 一共减k次
- 尾数的舍入处理
- 在对阶和尾数右规时,可能会对尾数进行右移, 为保证运算精度一般将低位移出的位保留下来参与中间的运算, 最后将运算结果进行舍入, 还原表示成IEEE754格式, 但也产生两个问题
- 保留多少附加位才能保证运算的精度
- IEEE754规定所有浮点数运算的中间结果右边都必须至少额外保留 两位附加位;
- 紧跟在浮点数尾数右边的那一位是 保护位或警戒位(guard), 用来保护尾数右移的位
- 紧跟保护位右边的是 舍入位(round), 左规时可根据其值进行舍入
- 为进一步提高计算精度, 在保护位和舍入位后面还引入了额外的一个数位, 称为 粘位(sticky), 只要舍入位的右边有任何非0数字, 粘位就被置为1否则置为0
- IEEE754规定所有浮点数运算的中间结果右边都必须至少额外保留 两位附加位;
- 最终如何对保留的附加位进行舍入(IEEE754提供4种可选模式)
- 就近舍入, 舍入为最近可表示的数. 当运算结果时两个克表示数的非中间值时实际上是"0舍1入"方式; 当结果正好在两个可表示数中间时,根据"就近舍入"的原则就无法操作了
- IEEE754规定该情况下结果强迫为偶数. 即: 若结果的LSB为1(奇数)时则末位加1; 若LSB为0(偶数)时则直接截取
- 就近舍入是目前计算机种默认的舍入方式
- 朝+∞方向舍入. 总是取右边最近可表示数, 也成为 正向舍入或朝上舍入
- 朝-∞方向舍入. 总是取左边最近可表示数, 也成为 负向舍入或朝下舍入
- 朝0方向舍入. 直接截取所需尾数, 丢弃后面所有位, 也成为 截取/截断或恒舍法.
- 处理简单, 无论正数负数, 都是取更靠近原点的那个可表示数, 是一种趋向原点的舍入, 又称为 趋向零舍入
- 就近舍入, 舍入为最近可表示的数. 当运算结果时两个克表示数的非中间值时实际上是"0舍1入"方式; 当结果正好在两个可表示数中间时,根据"就近舍入"的原则就无法操作了
- 保留多少附加位才能保证运算的精度
- 在对阶和尾数右规时,可能会对尾数进行右移, 为保证运算精度一般将低位移出的位保留下来参与中间的运算, 最后将运算结果进行舍入, 还原表示成IEEE754格式, 但也产生两个问题
- 阶的溢出判断
- 尾数规格化和尾数舍入可能会对结果的阶码执行加减运算, 需要考虑结果阶的溢出问题.
- 若一个正阶超过了最大允许值(127或1023)则发生 阶上溢, 机器产生
阶上溢异常 - 浮点数加减运算过程可知, 浮点数的溢出并不以尾数溢出来判断, 尾数溢出可通过右规操作得到纠正
- 运算结果是否溢出主要看结果的阶是否发生了上溢.
浮点数加减运算例子
用IEEE754单精度浮点数加减运算计算 0.5+(-0.4375).
解: 设 \(x=0.5=0.100…0B=(1.00…0)_2×2^{-1},y=-0.4375=-0.01110…0B=(-1.110…0)_2×2^{-2}\)
用IEEE754单精度格式表示为: $$ [x]_浮 = 00111111000…0, [y]_浮=101111101110…0 $$
得出, \( [E_x]_移 = 01111110(-2),M_x=0(1).000…0, [E_y]_移 = 01111101(-3),M_y=1(1).110…0 \)
尾数\( M_x和M_y种小数点前两位有两位, 第一位是"数符", 第二位加了括号是隐藏位"1" \)
计算机进行浮点数加减运算的过程如下(假定保留2位附加位 : 保护位和舍入位)
- 对阶
\( [\Delta E]_补=[E_x]_移+[-[E_y]_移]_补 (mod 2^n)=01111110+10000011=0000 0001 \)
得出\( \Delta E=1 \), 所以需要对y进行对阶, 即y的尾数\( M_y \)右移一位,符号位不变, 数值高位补0, 隐藏位右移到小数点后面, 最后移出的位保留两位附加位,结果为
\( E_b=E_y=E_x=01111110, M_y=10.(1)110…000 \)
- 尾数相加
\( M_b=M_x+M_y=01.0000…000+10.1110…000(小数点在隐藏位后) \)
根据原码加减运算规则, 结果为 01.0000…000+10.1110…000=00.00100…000(最左边的第一位是符号位, 其余是数值部分,尾数(最)后面两位是附加位)
- 规格化
所得尾数的数值部分高位有3个连续0所以需要进行左规操作. 即将尾数左移3位,并将阶码减3.
尾数左移是数值部分最左3个0被移出, 小数点右移了3位后移到了第一位1后面(隐藏位), 因此得 \( M_b=0(1).00…000000 \)
\( 阶码E_b=E_b-3=(((01111110-00000001)-00000001)-00000001)=0111 1011 \)
计算机中, 每次减1可通过加 \( [-1]_补(即"+11111111") \)来实现
- 舍入
把结果的尾数\(M_b\)中最后多余的两位舍入, 从本例来看, 不管用什么舍入法结果都一样, 都是把最后两个0去掉, 得 \( M_b=0(1).00…0000 \)
- 溢出判断
上述阶码计算和调整过程中, 没有发生阶码上下溢得问题, 因此阶码 \( E_b=0111 1011 \)
最终得到结果为 \( [x+y]_浮=00111101100…0 \)
因为 01111011B=123, 所以阶码的真值为 123-127=-4, 尾数的真值为+1.0…0B=+1.0, 所以\(x+y=1.0✖2^{-4}=1/16=0.0625\)
2.10.2 浮点数乘/除运算
- 浮点数乘除运算前应对参加运算的操作数进行判0处理,规格化操作和溢出判断, 确定参加运算的操作数是正常的规格化浮点数
- 与加减相比, 浮点数乘除不需要对阶操作, 其他一样
- 已知两个浮点数\( x=M_x×2^{E_x},y=M_y×2^{E_y} \),则乘除结果如下
- \( x×y=(M_x×2^{E_x})×(M_y×2^{E_y})=(M_x×M_y)×2^{E_x+E_y} \)
- \( x÷y=(M_x×2^{E_x})÷(M_y×2^{E_y})=(M_x÷M_y)×2^{E_x-E_y} \)
- 浮点数乘法运算
- 假定x和y是两个IEEE754标准规格化浮点数, 相乘结果为 \( M_b×2^{E_b}, 则求M_b和E_b的过程如下 \)
- 尾数相乘, 阶码相加
- 尾数的乘法运算\( M_b=M_x×M_y \), 可采用定点原码小数乘法.
- 运算时需将隐藏位1还原到尾数中,且要注意乘积小数点的位置
- 阶的相加运算\( E_b=E_x+E_y \), 采用移码相加运算
- 尾数规格化
- 对于IEEE754标准的规格化尾数\( M_x和M_y, 一定要满足条件 : |M_x|≥1,|M_y|≥1, 因此两数乘积绝对值应满足 : 1≤|M_x×M_y|<4 \)
- 数值部分得到的2n位乘积bb.bb…b中小数点左边一定至少有一个1,可能是01,10,11三种情况.
- 01 : 不需要规格化
- 10或11 : 右规一次,此时\( M_b右移一位,阶码E_b加1 \)
- 规格化后得到的尾数数值部分的形式为 01.bb…b,小数点左边的1是隐藏位
- 对于IEEE754浮点数的乘法运算不需要进行左规处理
- 尾数舍入处理
- \( 对M_x×M_y \)规格化后得到尾数形式为±01.bb…b其中小数点后有(2n-2)位尾数积, 最终结果只能有24位尾数(单精度)或53位尾数(双精度)
- 浮点数乘积的低位部分舍入与加减运算中的舍入操作一样
- 阶码溢出判断
- 阶相加,右规和舍入时需要对阶进行溢出判断
- 溢出判断与浮点数加减运算的溢出判断方法一样
- 浮点数除法运算
- 尾数相除,阶码相减
- 尾数的除法运算\( M_b=M_x÷M_y \), 可采用定点原码小数除法.
- 运算时需将隐藏位1还原到尾数中,且要注意乘积小数点的位置
- 阶的相减运算\( E_b=E_x-E_y \), 采用移码相减运算
- 尾数规格化
- 对于IEEE754标准的规格化尾数\( M_x和M_y, 一定要满足条件 : |M_x|≥1,|M_y|≥1, 因此两数相除的绝对值应满足 : 1/2≤|M_x/M_y|<2 \)
- 数值部分得到的n位商 b.bb…b中小数点左边的数可能时0也可能时1.
- 0 : 小数点右边第一位一定时1, 需要左规一次, 即\( M_b \)左移一次,阶码\( E_b \)减1
- 1 : 结果就是规格化形式
- 对于IEEE754浮点数的除法运算不需要进行右规处理
- 尾数舍入处理
- \( 对M_x/M_y \)规格化后得到尾数形式为±1.bb…b其中小数点后n-1位尾数商,所以要对商的低位部分进行舍入,方法与加减运算的舍入操作一样
- 阶码溢出判断
- 阶相减,左规和舍入时需要对阶进行溢出判断
- 溢出判断与浮点数加减运算的溢出判断方法一样
本章小结
- 无符号数时正整数一般用于表示地址
- 带符号整数一般用补码表示, 浮点数表示实数大多用IEEE754标准表示
- 数据的排列有大端和小端两种;
- 大端以MSB所在地址位数据的地址, 即给定地址存放的是数据最高位有效字节
- 小端以LSB所在地址为数据的地址, 即给定地址存放的是数据最低位有效字节
- 定点运算由专门的定点运算器实现, 核心部件是带快速加法器的ALU
- 定点数运算包括移位运算, 扩展运算和加减乘除运算
- 补码加减用于整数加减运算, 符号位和数值位一起运算, 减法用加法实现
- 同号相加时若结果的符号不用于加数的符号则发生溢出
- 原码加减用于浮点数尾数加减运算
- 乘法运算用重复进行加法和右移实现
- 补码乘法用于带符号整数乘法运算, 符号位和数值位一起运算
- 原码乘法的符号位和数值位分开运算, 数值部分用无符号数乘法实现
- 除法运算用重复进行加减和左移实现
- 浮点数运算由专门的浮点运算器实现
- 加减运算需要经过 对阶/尾数相加减/规格化/尾数舍入/溢出判断(阶)
- 乘除运算, 尾数用定点数乘除运算实现,阶码用定点数加减实现